摘 要

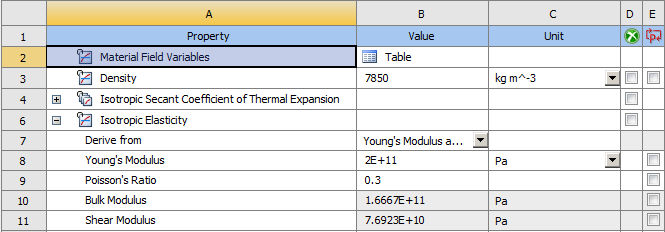
本文根据已给的动力学、热力学计算条件，设计出CD4108发动机曲轴，利用CATIA软件对其进行三维实体造型；应用ANSYS Workbench中的Static Structural对曲轴进行有限元分析，根据动力学计算得到的载荷及约束边界条件，计算得到曲轴在受最大载荷时的等效应力和总变形量分布图，并指出各缸最大爆发压力下曲轴的薄弱部位，提出了优化措施。同时，利用ANSYS Workbench中的Model（模态分析）模块对曲轴进行了自由状态下的模态分析，从而得到曲轴的固有频率和振型。

结果显示，曲轴的最大应力多出现在爆发缸的连杆轴颈与曲柄连接处或者主轴颈与平衡重的连接处，最大变形量位于爆发缸的连杆轴颈的中心处；根据曲轴有限元自由模态分析，本文研究的曲轴最低固有频率远远高于基频，有效避开了共振频率。

关键词：曲轴；ANSYS Workbench；有限元分析；强度；模态分析

Abstract

In this paper, according to the given dynamic and thermodynamic calculation conditions, the crankshaft of CD4108 engine is designed and modeled by CATIA software. The finite element analysis of crankshaft is carried out by using the static analysis module of ANSYS Workbench. According to the load and constraint boundary conditions obtained by dynamic calculation, the distribution diagrams of equivalent stress and total deformation of crankshaft under maximum load are calculated. The weak position of crankshaft under maximum burst pressure of each cylinder is pointed out, and the optimization measures are put forward. At the same time, the modal analysis of the crankshaft in the free state is carried out by using the Mode module of ANSYS Workbench, and then the natural frequency and vibration mode of the crankshaft are obtained.

 The results show that the maximum stress of the crankshaft mostly occurs at the connection between the connecting rod journal and the crank or between the main journal and the balance weight. The maximum deformation is in the center of the connecting rod journal of the explosive cylinder. According to the finite element free modal analysis of the crankshaft. The minimum natural frequency of the crankshaft studied in this paper is much higher than the fundamental frequency, which effectively avoids the resonance frequency.

Key words: crankshaft; ANSYS Workbench; finite element analysis; strength; model analysis

目录

摘要 I

Abstract II

第1章 绪论 1

1.1 课题研究的意义 1

1.2国内外曲轴研究现状 1

1.3课题主要研究内容 3

第2章 CD4108发动机相关计算 4

2.1 柴油机结构设计参数 4

2.1.1 初始条件 4

2.1.2 发动机类型 4

2.1.3 基本参数 4

2.2 热力学计算 5

2.2.1 热力循环基本参数 6

2.2.2 理论P-V图的绘制 6

2.2.3 实际P-V图的绘制 7

2.3 运动学计算 9

2.3.1 曲柄连杆机构的类型 9

2.3.2 连杆比的选择 9

2.3.3 活塞运动规律 9

2.3.4 连杆运动规律 10

2.4 动力学计算 11

2.4.1 连杆质量转换 11

2.4.2 气体力Fg 11

2.4.3 往复惯性力F 12

2.4.4 曲轴载荷计算 13

2.5 本章小结 15

第3章 曲轴模型的建立 16

3.1几何模型的建立（曲轴主要参数） 16

3.2有限元模型的建立 17

第4章 曲轴有限元分析 18

4.1有限元模型的建立 18

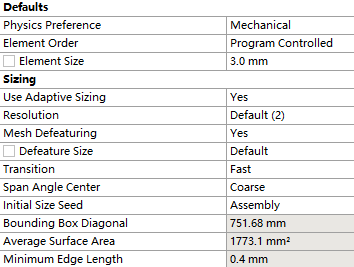
4.1.1网格划分 18

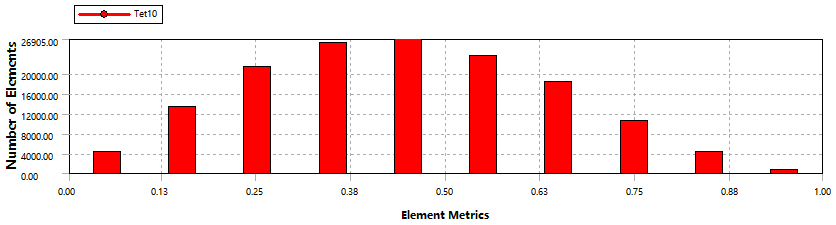
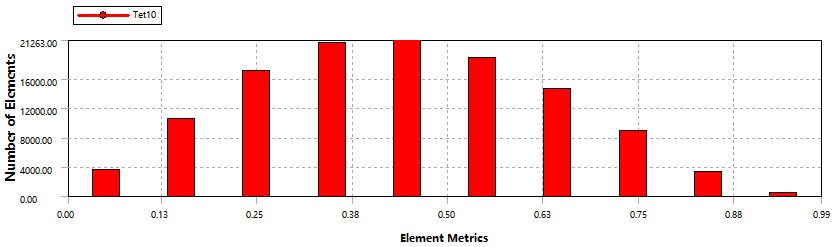
4.1.2网格质量检查 19

4.1.3调整网格划分 19

4.2边界条件 21

4.2.1转速条件 21

4.2.2连杆轴颈载荷 21

4.2.3曲轴扭转载荷 22

4.2.4曲轴支撑约束 23

4.3求解结果分析 23

4.3.1一缸点火结果分析 23

4.3.2二缸点火结果分析 24

4.3.3三缸点火结果分析 25

4.3.4四缸点火结果分析 26

4.3.5计算结果分析 27

4.3.6加密收敛分析 28

4.4本章小结 30

第5章 曲轴自由模态分析 31

5.1网格划分 31

5.2约束条件 31

5.3参数设置 31

5.4结果分析 32

5.5本章小结 35

第6章 总结 36

6.1结论 36

6.2展望 36

参考文献 37

致谢 38

绪论

1.1 课题研究的意义

随着汽车工业的快速发展，柴油机逐渐朝着高速、重载、轻型和大功率的方向发展，这也使得发动机曲轴的工作环境也愈来愈苛刻。曲轴是汽车发动机中最关键的零件之一。在发动机工作过程中，曲轴承受着周期性变化的缸内气体压力、活塞组往复和旋转质量惯性力及其他不规则阻力矩和外界反作用力。由于曲轴长期工作在拉压、弯曲和扭转等应力状态下，在形状突变处容易产生应力集中，从而使曲轴形成局部的疲劳裂纹，严重甚至会导致曲轴断裂。一旦曲轴失效，发动机其他零部件就会相应在工作过程中被破坏，造成无法估量的严重后果。因此，为了发动机能够正常、安全地运行，曲轴能够不发生失效，其必须要有足够的强度和刚度，从而在危险截面既不会产生裂纹，也不会出现过大变形。另外，曲轴自身的固有频率应该与激振频率避开，因为一旦当两者一致或者相接近时，就会产生共振，同样会使曲轴产生失效。因此，对已设计的曲轴进行有限元分析和自由模态分析就显得十分有必要。曲轴实物图如图1.1所示。

图1.1 曲轴实物图

1.2 国内外曲轴研究现状

在曲轴优化设计研究和三维实体造型及动力学参数优化设计研究方面，国内学者做了大量工作，徐中明等人针对曲轴的失效利用仿真技术进行了静力学强度分析，李德水等人采取试验的方法对小型柴油机曲轴的振动模态进行了分析研究，王良国等人对368Q型发动机曲轴进行了疲劳强度有限元分析，尹必峰、刘胜吉、潘文东等人通过普遍使用的AutoCAD软件对295直喷式柴油机曲轴进行三维实体造型，论述了三维实体造型的一般性方法^[1]；刘向军等人用ADVISOR软件对车用发动机进行动力匹配分析，从而得出国内发动机的不足，突出车辆匹配的重要性^[2]；陈然、曹咏弘、孙华东等人利用PRO/E建立内燃机曲轴的简化模型，并导入ANSYS进行模态分析，得出曲轴除了要有足够的刚度，强度和韧度外，还应具有很好的平衡性^[3]；李倩等人根据曲轴的对称性，利用UG软件提供的“镜像体”命令对曲轴造型，提高了作图速度^[4]；景银萍、崔志琴、刘威、黄坤等人利用灵敏度分析法、优化算法和设计参数法相结合的方法，对曲轴模型进行动力学参数优化设计，使曲轴的动力学模型与实际更吻合^[5]；商海昆、支亚辉、冯国胜、胡春萍、钱超、孙晓伟等人利用Solidworks建立曲轴的三维实体模型，运用ANSYS Workbench的静力分析模块和Fatigue tool工具箱，对曲轴在各缸最大爆发压力下的强度和可靠性进行分析，得出各缸爆发时的最大应力位置均出现在爆发缸所在的两个相邻轴颈连接处，即连杆轴颈过度圆角处^[6]；文怀军、闫雪华等人通过有限元方法得到将曲轴材料由锻钢改为球墨铸铁的设计及优化方案^[7]；石来华等人应用发动机一维模拟软件GT-POWER建立某四缸车用汽油机工作过程的计算分析模型，计算发现优化进气系统后发动机的中、高转速区域的动力性能得到了较大改善，但对发动机低转速的动力性能的改善作用不大^[8]；凌建群等人建立汽车加速过程消耗的计算方法，结果得出无论直接挡加速还是起步换挡加速加速油耗和加速时间都成反比的关系^[9]；贺洋洋、申琪、郭昌盛、张昌明、熊超、邢思等人利用CATIA软件对汽车发动机曲轴进行参数化建模，并结合ANSYS Workbench软件进行有限元分析，对曲轴进行优化设计，得到曲轴的最优参数^[10]；国外学者V.Mallikarjuna Reddy、T.Vijaya Devi等人利用Unigraph-NX7.5对曲轴进行建模，并利用有限元分析软件ANSYS对曲轴进行结构分析，发现在最大应力极限下，曲轴的强度有所提高，随着曲轴重量的减小，曲轴的成本降低，发动机性能提高^[11]；Paolo Citti、Alessantro Giogetti、Ulisse Millefanti等人介绍并展示了一种用于高性能曲轴的新型贝氏体低碳含量的表征相，收集并评价了渗氮效果(氮扩散)的表面硬化和显微硬度分布^[12]；Xiaio-lei Xu、Zhi-wei Yu等人得出卡车发动机曲轴断裂发生在曲轴大端，正时齿轮和飞轮法兰耦合在一起，断裂位置正好位于两者之间的装配间隙^[13]；Joao Gomes、Narciso Gaivota、Rui F.Martins等人在Soderberg准则下对曲轴的理论尺寸进行评估，并利用有限元方法对曲轴模型在整个燃烧循环中的几个应力集中区域进行分析，得出曲轴发生故障的原因^[14]；G.Kinal、J.Musial、M.Szczutkowski等人对轴承与轴颈表面的磨损进行研究，在代表轴颈的套筒上使用光栅法钻EN-GJS-600球墨铸铁，可以得到厚度为0.3 mm的表层熔化区的特点是断面显微硬度分布均匀，硬化区显微硬度逐渐降低^[15]。

1.3 课题主要研究内容

三维造型的准确性、造型的快慢直接影响曲轴的生产质量和周期，研究曲轴的造型设计不仅对提高汽车产品的质量具有重要意义，同时对缩短相关产品的生产周期具有重要意义。由于曲轴是发动机中典型的易损件之一，其强度和振动特性都会影响到整机的工作性能，因此对曲轴进行有限元分析，研究曲轴的应力和应变状态，了解其固有频率和模态振型，对于设计和优化曲轴结构有重要意义。论文主要研究内容如下：

（1）使用EXCEL公式模块，进行对于发动机结构设计参数的确定，以及热力学计算和动力学计算，针对热力学计算，所需参数可通过查阅《内燃机原理》和《工程热力学》选取，同时综合考虑喷油提前角、最高爆发压力等影响因素；

（2）参考文献《柴油机设计手册》的相关说明，对曲轴结构进行具体设计；利用CATIA和CAD这两个绘图软件绘制曲轴的零件图；曲轴的建模使用CATIA，建模时，在不影响有限元分析的前提下应尽可能的简化曲轴结构，并且由于曲轴是对称的，可以只用曲轴的一半模型进行分析；

（3）曲轴的有限元分析，使用ANSYS Workbench，由于只是做强度校核，因此只考虑在最大拉力和最大压力的情况下，曲轴的应力和应变情况，其中应力情况包括曲柄销径向力和切向力、过渡圆角上的应力集中。

CD4108发动机相关计算

2.1 柴油机结构设计参数

2.1.1 初始条件

额定功率参考玉柴增压4108发动机，取Pe=110kW

平均有效压力：pme=0.8~1.2MPa

活塞平均速度：vmlt;18m/s

2.1.2 发动机类型

参考同类型发动机，本次设计选用四冲程内燃机，即τ= 4。

参考同类型发动机，本次课题选用水冷方式。

参考同类型发动机，本次课题选用直列四缸内燃机。

2.1.3 基本参数

根据内燃机学的基本计算公式：

其中Pe —— 为发动机的有效功率，定为110kW；

Pme—— 为内燃机的平均有效压力，根据《内燃机设计》取为1MPa；

Vs—— 为气缸的工作容积，单外为升（L）；

i —— 为发动机的气缸数目，其值为4；

n —— 为发动机的转速，单位为r/min；

—— 活塞的平均速度，参考《内燃机学》取为10m/s；

S —— 内燃机活塞的行程，单位为毫米（mm）；

D —— 内燃机气缸直径，单位为毫米（mm），，由题目定为108mm；

τ—— 发动机的行程数，依题取为4。

根据以上的条件带入公式求得：

D=108 mm，

S=115 mm，

n=2608.70 r/min，

Vs=1.053 L，

将n取整为2600r/min

根据计算得出的D和S计算实际的单杠排量、行程缸径比、平均有效压力和活塞平均速度，得：

Vs=1.053 L，

pe=1.2053 MPa，

vm=9.9667 m/s。

2.2 热力学计算

活塞式内燃机的理想循环分为三类，即混合加热循环理想循环（萨巴德循环）、定压加热理想循环（狄赛尔循环）、定容加热理想循环（奥托循环）。柴油机实际循环近似看成混合加热循环理想循环。在本设计过程中，先确定热力循环基本参数然后进行热力学计算，绘制P-V图。为建立内燃机理论循环，需对内燃机的实际循环中大量存在的湍流耗散以及温度压力分布不均匀等一系列不可逆损失作必要地简化和假设，归纳起来有以下几点：

假设工质是理想气体，其物理常数与标准状态下的空气物理常数相同；

忽略发动机进排气过程，将实际的开口循环简化为闭口循环；

假设工质的压缩及膨胀是可逆过程；

假设燃烧过程为混合加热过程，工质放热过程为定容放热。

2.2.1 热力循环基本参数

取压缩过程绝热指数：

=1.36

取膨胀过程绝热指数：

=1.22

根据参考文献《内燃机原理》P29增压柴油机压缩比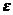=11~17，取几何压缩比为

=17

根据参考文献《工程热力学》取定容增压比

λ=1.45

根据参考文献《工程热力学》取初始膨胀比

ρ=2.2

根据参考文献《工程热力学》选取大气压力

=0.1013MPa

2.2.2 理论P-V图的绘制

通常情况下，压缩始点的压强在P1=（0.8～0.9）Po（Po为当地大气压力值），假选定P1=0.09MPa，将压缩过程近似看作可逆多变过程，由上一步n1=1.36，并利用PVn=const，利用前面计算所得单缸容积，可以在Excel中绘出压缩过程线。混合气体在气缸中压缩后，先经等容加热，利用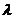值可得最大爆发压力值，然后进行等压加热，利用初期膨胀比可以确定该过程的终点气缸工作容积。膨胀过程类似于压缩过程，n2由上一步取得1.22，绘出膨胀线。最后连接膨胀终点和压缩始点，即可得出理论循环的P-V图。计算过程如下：

1）压缩段：

压缩始点：P1=0.152 MPa，V1=1.1778 L；

压缩终点：P2=6.7333 MPa，V2=0.0785 L；

2）定容加热段：

定容始点：P2=6.7333 MPa，V2=0.0785 L；

定容终点：P3=P2×λ=9.7633 MPa，V3=0.0785 L；

3）等压加热段：

等压始点：P3=9.7633 MPa，V3=0.0785 L；

等压终点：P4=9.7633 MPa，V4= V3×ρ=0.1727 L；

4）膨胀段：

膨胀始点：P4=9.7633 MPa，V4=0.0785 L；

膨胀终点：P5=0.6644 MPa，V5=1.1778 L；

绘图采用描点绘图法，以V（体积，单位L）为横坐标，对应的P（缸内压力，单位MPa）为纵坐标，绘制各段曲线，再将膨胀终点和压缩始点相连，即可得到理论P-V图。

2.2.3 实际P-V图的绘制

实际的P-V图和利用多变过程状态方程绘制的P-V图还存在一些差别，在柴油机中，为了使其动力性、经济性达到最优，采取了喷油提前，配气正时。从《内燃机学》、《内燃机原理》中可知主要是喷油提前角和燃烧的原因。

在理想循环中，工质在气缸中是均匀的，由于定容加热是瞬时完成的，定压加热是在P3-P4阶段内完成的，所以，其示功图的上方呈方角形。在实际循环中，燃烧是不可能瞬时的，它必然需要一定的时间才能完成这一过程。由于常在上止点前喷油、着火，因此，在压缩行程终了前，活塞在压缩行程末期要承受较大的压缩功；到了上止点后，活塞开始下移，燃烧继续进行，它先使压力线偏离纵坐标轴向外向上引申，达到最高压力点后，又使压力线向外向下延伸与膨胀线圈圆滑相接，所以，其示功图的上方呈圆弧形，从而减小了部分示功图面积。这就是由于燃烧不及时在压缩行程末端和燃烧的最大压力处引起的损失。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：