Hamilton体系下的动力学方程辛求解算法毕业论文
2020-02-19 09:51:14
摘 要
随着科学与技术的发展,在航空航天技术和机器人设计中,以及其他轻量化,高精度的工业设计中,近些年来对动力学方程的研究令人瞩目。有着广泛的应用前景。
对于动力学方程。本文对于常用的描述和求解方法:直接积分法,中心差分法,Houbolt法,Wilsonθ法,Newmark法,振型叠加法作了一定的分析和研究
这些强有力的算法尽管非常有效。局限性也相当明显。由于算法本身耗散系统的能量并使得动态响应的相位滞后。通过减小步长所带来的计算量问题相当棘手。
辛求解算法可以有效解决动力学方程问题。进一步通过研究Hamilton体系的数学基础。导出约束哈密顿系统的运动方程,用投影R-K方法,该方法通过将R-K方法与投影技术相结合来保留三个级别的约束和能量。建立了一个预测的R-K方法来解决动力学方程。该方法可以保留三个级别的约束以及约束哈密顿系统的总能量。 然后应用投影来校正答案,以满足三个级别的约束方程并保持能量。
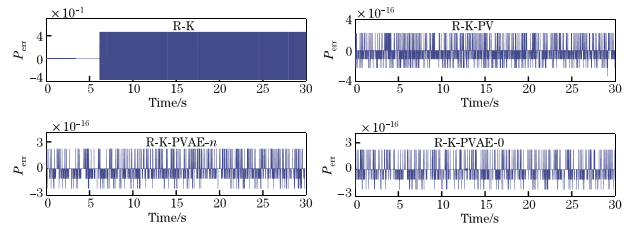
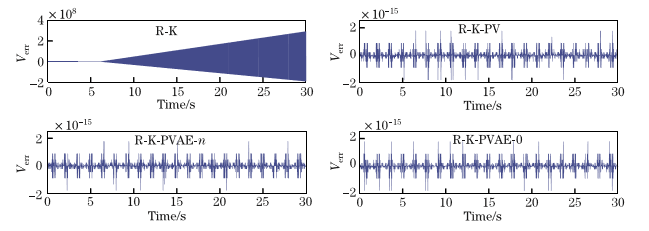
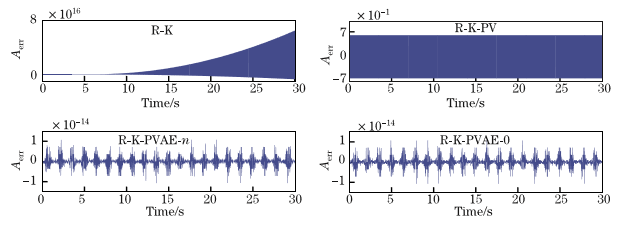
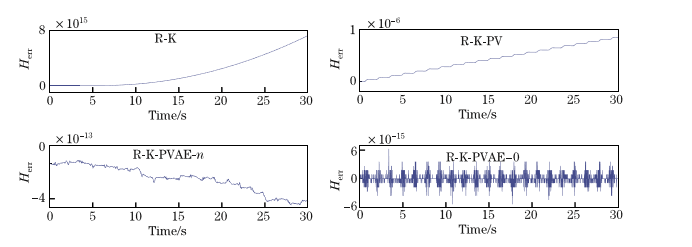
通过数值分析,该方法不仅在位置和速度上上具有良好的保持约束的能力,而且在约束哈密顿系统的加速度上和总能量方面具有良好的能力。 同时,数值实验表明,该方法的优点是长期稳定。
关键词:动力学方程 ;Hamilton系统;Runge-Kutta算法;辛算法
Abstract
With the development of science and technology, in the aerospace technology and robot design, as well as other lightweight, high-precision industrial designs, the research on dynamic equations has been remarkable in recent years. Has a wide range of application prospects.
For the kinetic equation. In this paper, the common description and solution methods: direct integration method, central difference method, Houbolt method, Wilson θ method, Newmark method, mode superposition method are analyzed and studied.
These powerful algorithms are very effective. The limitations are also quite obvious. Since the algorithm itself dissipates the energy of the system and causes the phase of the dynamic response to lag. The computational problem caused by reducing the step size is quite tricky.
The symplectic solution algorithm can effectively solve the dynamic equation problem. Further study the mathematical basis of the Hamilton system. The equations of motion for constrained Hamiltonian systems are derived using the projected R-K method, which preserves three levels of constraints and energy by combining the R-K method with projection techniques. A predictive R-K method was developed to solve the dynamic equations. This method preserves three levels of constraints and constrains the total energy of the Hamiltonian system. The projection is then applied to correct the answer to satisfy the three levels of constraint equations and maintain energy.
Through numerical analysis, the method not only has good ability to maintain constraints in position and speed, but also has good ability in constraining the acceleration and total energy of the Hamiltonian system. At the same time, numerical experiments show that the advantage of this method is long-term stability.
Key Words:Dynamic equation; Hamilton system; Runge-Kutta algorithm; symplectic algorithm
目录
摘要 3
第一章 绪论 6
1.1. 引言 6
1.2. 研究现状 6
1.2.1. 动力学方程与数值算法 6
1.2.2. Hamilton原理与辛算法 7
1.2.3. 本文的主要工作 7
第二章 8
2.1. 动力学方程 8
2.2. 动力学方程的求解方法 10
2.2.1. 积分法 10
2.2.2. 振型叠加法 17
第三章 Hamilton系统下的Runge-Kutta方法 20
3.1. 约束Hamilton系统的控制方程 20
3.2. 投影的Rung-kutta方法 21
3.2.1. R-K方法 21
3.2.2. 投影的R-K方法 23
3.3. 数值例子 26
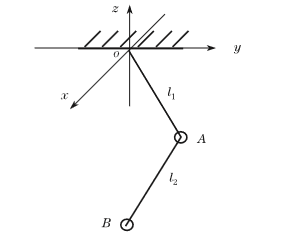
3.3.1. 球型单摆 26
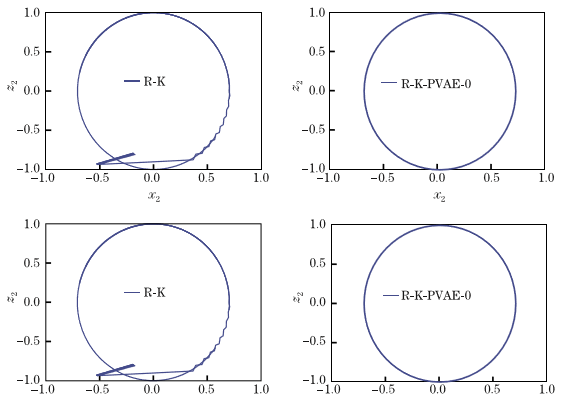
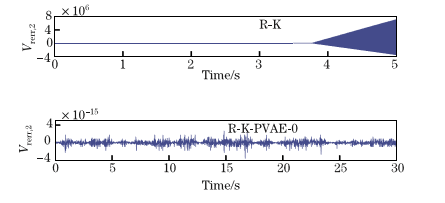
3.3.2. 双球型摆 29
第四章 总结与展望 31
4.1. 总结 31
4.2. 未来展望 32
绪论
引言
柔性系统动力学是这些年来新近发展起来的一门新兴学科。【1】【2】它是现代物理基础理论如结构动力学,计算力学和数值计算方法与计算机科学技术等学科构成的一门学科。是较强的交叉型学科研究领域。它在机器人供工业领域,航空航天领域。在机械系统向着轻量化,高速化以及高精度方向发展。因此传统的将多体系统按照刚体来处理已经不能满足要求了。迫切需要新的理论支持来解决问题。如卫星及航天器的飞行的稳定性问题。高速轻型路面汽车。机器人的运作。以及高精密的机床系统设计等等。【3】在某种层面上讲。它在一定程度上反映了国家高科技的水平。有巨大的理论价值和应用层面意义。【4】
目前,尽管对于系统动力学的研究已经取得了一定的进展,但是存在的问题依然非常多。例如,对于约束的多体系统动力学的越苏违约造成的数值计算稳定性问题。对于高速运动的 系统在系统建模中存在的刚度项丢失而造成的计算结果失真等问题。是柔性系统动力学的一个主要瓶颈问题。柔性系统动力学方程是计算数学里的具有很大刚性比的常微分-代数方程。方程的刚性问题会给求解系统响应带来很大的困难。所以寻找高精度,稳定性的数值计算方法是解决问题的一个还非常重要的方面。【5】【6】
研究现状
柔性多提系统动力学研究就目前状况来看。共有三类研究方法:实验方法,解析方法。和实验方法。三者方法互相验证互相借鉴。各有其局限性。考虑到实际应用情况。数值分析方法是用的最广,最有生命力的方法
动力学方程与数值算法
数值方法在研究中有着非常重要的作用。其关键在于高效,高精度的计算过程。对P.W.Likins 在上个实际七十年代研究了卫星动力学问题。他最先采用混合坐标来模拟系统。后来被广泛应用到多 系统动力学中。【7】
Kimisey讨论了有关于撞击动力学的数据结构和算法。对于含有撞击的柔性多体系统动力学问题。一般采用动量平衡法。通过引入拉格朗日乘子。利用增广法来进行求解问题。对于直接通过数值积分进行计算。常见的算法有Runge-Kutta法【8】,Newmark法【9】,Newton-Raphson法,Wilson 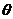 法,Gear法。等等
法,Gear法。等等
由于这些强有力的算法本身耗散系统的能量并且使得动态响应的相位滞后。因此其长期追踪能力不是很理想,不太令人满意。虽然可以通过减小步长来达到降低耗散减小相位滞后的情况。通过这种方法来达到提高计算精度的目的,但是这个去仍要以付出巨大的工作量。在工程应用上可能吃不消。因此还需要寻找更好的数值计算方法
Hamilton原理与辛算法
Hamilton力学和拉格朗日力学,以及牛顿力学是历史上经典力学的三个历史性里程碑
Hamilton体系是现代动力系统的重要体系。Hamilton体系应用广泛。包括天体力学,星系力学。分子佛南管理学,控制理论,量子力学。一切真实的,有耗散的物理过程都可以表示成Hamilton形式【10】
Hamilton体系是在1834年提出。后来著名数学家Jacobi给出了哈密尔顿-雅可比方程。在非常经典的《经典力学的数学方法》中详细论述了和Hamilton体系和数学框架-辛几何的。【11】
在我国,以冯康院士为代表的学者在提出有限元法之后,提出了在Hamilton体系下的辛几何算法。这是我国为世界科学的卓越贡献。冯康和秦孟兆在《哈密尔顿系统的辛几何算法》中系统的阐述了哈密尔顿系统栓发的重要研究成果。包括辛代数和辛几何。哈密尔顿力和辛几何。构建了完整的辛几何的算法的的理论框架。讨论了算法守恒性,守恒性之间的相互关系。推广了辛算法思想。实现了动力系统算法的理论几何化。在学术上作出了卓越贡献。【12】【13】
1993年钟万勰院士等针对动力系统建模和计算问题,在动力系统原变量的基础上提出了,引入偶变量,提出辛对偶体系。建立了Hamilton动力体系的辛几何理论和时程精细积分理论。将位移坐标模拟成时间,从而实现辛求解。【14】
Mclachlan提出应用向量场的雅可比矩阵的“牛顿-泰勒”迭代法求解Runge-Katta隐式方程。【15】通过减少在每一步中的向量求职。使得对于积分时间很长的辛Punge-Katta方法的效率大大提升【16】。MIguel Preto提出了步长自适应辛格式算法【17】。适用于哈密尔顿函数是系统动能和势能之和且时间步仅以来势能的类型
本文的主要工作
本文主要研究Hamilton体系下的辛算法。柔性系统动力学方程由于其特点主要依靠数值求解来得到。Hamilton体系下的Runge-kutta算法是在隐士R-K方法的基础上发展的。在Hamilton体系中是辛矩阵辛算法格式推进。能够保持相空间结构。文章中,用一种投影R-K方法,该方法通过将R-K方法与投影技术相结合来保留三个级别的约束和能量。
本文分为以下几个部分:
第一章 通过概述了系统动力学的主要问题和现状。高精度的算法是主要的方法。同时介绍Hamilton体系以及辛算法产生,发展,和研究现状
第二章 阐述动力学方程的系统建模和常见的传统的数值方法以及相应的局限性。
第三章 研究Hamilton体系的数学基础。导出约束哈密顿系统的运动方程,用影R-K方法,该方法通过将R-K方法与投影技术相结合来保留三个级别的约束和能量。建立了一个预测的R-K方法来解决动力学方程。 通过数值结果来说明辛算法在求解系统动力学的有效性。
第四章 对全文工作进行反思总结并提出进一步的展望。
动力学方程
描述动力学特征的基本力学变量和方程与静力问题类似,但所有的变量都是时间的函数。
基本变量
三大类变量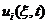 、
、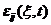 和
和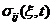 是坐标位置
是坐标位置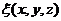 和时间
和时间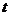 的函数,一般将其记为
的函数,一般将其记为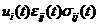 。
。
平衡方程
利用达朗贝尔原理将惯性力和阻尼力等效到静力平衡方程中,有
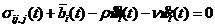 (1)
(1)
其中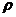 为密度,
为密度,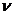 为阻尼系数。
为阻尼系数。
几何方程
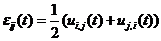 (2)
(2)
物理方程
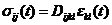 (3)
(3)
其中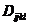 为弹性系数矩阵。
为弹性系数矩阵。
边界条件
位移边界条件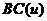 为,
为,
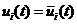 在
在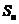 上 (4)
上 (4)
力的边界条件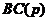 为,
为,
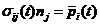 在
在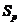 上 (5)
上 (5)
初始条件
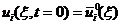 (6)
(6)
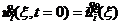 (7)
(7)
虚功原理
基于上述基本方程,可以写出平衡方程及力边界条件下的等效积分形式,
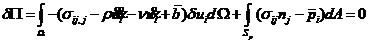 (8)
(8)
对该方程右端第一项进行分部积分,并应用高斯-格林公式,整理得,
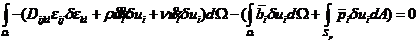 (9)
(9)
有限元分析列式
单元的节点位移列阵为,
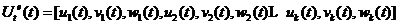 (10)
(10)
单元内的插值函数为,
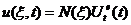 (11)
(11)
其中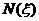 为单元的形状函数矩阵,与相应的静力问题单元的形状函数矩阵完全相同,
为单元的形状函数矩阵,与相应的静力问题单元的形状函数矩阵完全相同,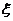 为单元中的几何位置坐标。
为单元中的几何位置坐标。
基于上面的几何方程和物理方程及(11)式,将相关的物理量表达为节点位移的关系,有,
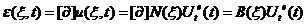 (12)
(12)
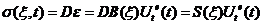 (13)
(13)
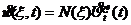 (14)
(14)
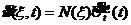 (15)
(15)
将(12)-(15)供稿到虚功方程(9)中,有,
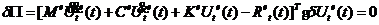 (16)
(16)
由于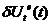 具有任意性,消去该项并简写有,
具有任意性,消去该项并简写有,
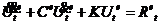 (17)
(17)
其中,
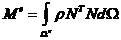 (18)
(18)
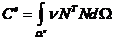 (19)
(19)
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: