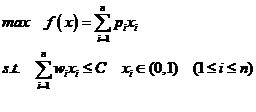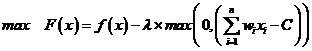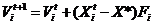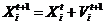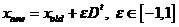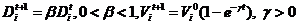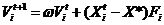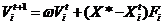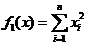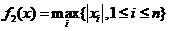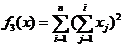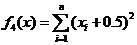基于改进蝙蝠算法的0-1背包问题求解研究毕业论文
2020-04-10 16:42:39
摘 要
本文借助蝙蝠算法(Bat Algorithm BA)对0-1背包问题进行了求解,运用优化的蝙蝠算法进行求解,比较了算法的优化能力和收敛能力。 BA具有结构简单,参数少,鲁棒性强,易于理解和实现等优点,已成功地运用到工程设计,分类,神经网络,模糊聚类等领域。
论文介绍了蝙蝠算法的优缺点,改进的蝙蝠算法及其应用,以及解决0-1背包问题的多目标优化问题。
本文的主要工作:提出了一种二进制蝙蝠算法和混合算法。它在解决KP问题上取得了很好的效果,有望运用于解决0-1背包问题的实际情况。
研究结果表明:混合算法可以很好的解决0-1背包问题,收敛速度快,精度高于其他群智能算法。
关键词:蝙蝠算法;改进的蝙蝠算法及应用;0-1背包问题;多目标优化
Abstract
In this paper, Bat Algorithm BA is used to solve the 0-1 knapsack problem, and the bat algorithm is optimized to solve it. The optimization ability and convergence ability of the algorithm are compared. BA has the advantages of simple structure, few parameters, strong robustness, easy to understand and realize, and has been successfully applied to engineering design, classification, neural network, fuzzy clustering and other fields.
The paper describes the advantages and disadvantages of the bat algorithm, the improved bat algorithm and its application, and the multi-objective optimization problem of 0-1 knapsack problem.
The results show that the hybrid algorithm can solve the 0-1 knapsack problem very well, the convergence speed is fast, and the accuracy is higher than other group intelligent algorithms.
This article features: This paper presents a binary bat algorithm and hybrid algorithm. It has achieved very good results in solving the KP problem and is expected to be applied to solve the actual situation of the 0-1 knapsack problem.
Key Words:Bat algorithm;Improved bat algorithm and application;0-1 knapsack problem;multi-objective optimization
目 录
摘要 I
Abstract II
目 录 1
第1章 绪论 1
1.1 蝙蝠算法的应用与发展现状 1
1.2 0-1背包问题的来源及求解应用 2
1.3 问题描述 2
第2章 蝙蝠算法及其应用 3
2.1 蝙蝠算法的原理 4
2.2 响度与脉冲速度 4
2.3 数值仿真 5
2.4 函数测试 6
2.5 小结 8
第3章 改进的蝙蝠算法求解0-1背包问题 9
3.1 二进制蝙蝠算法 9
3.2 二进制蝙蝠算法求解0-1背包问题 10
3.3 小结 11
第4章 求解0-1背包问题的原混合遗传算法 12
4.1 原混合遗传算法 12
4.1.1 编码方法 12
4.1.2 贪心算法的应用 12
4.1.3 适应度函数 12
4.1.4 遗传算子的选用 13
4.1.5 算法步骤 13
4.2 用改进的原混合遗传算法求解0-1背包问题 13
4.2.1 贪心算法的步骤 13
4.2.2 变异算子 14
4.2.3 终止条件 15
4.2.4 算法步骤 15
4.3带值计算及实验结果分析 16
4.3.1 带值计算 16
4.3.2 实验结果分析 17
4.4 结论 18
参考文献 18
致 谢 20
绪论
蝙蝠算法模拟了微型蝙蝠回声定位的原理,该算法使用频率调谐技术来改善人群中解决方案的多样性。 自动缩放技术用于动态改变脉冲发射率和脉冲响度,以平衡搜索过程中全局优化和局部优化之间的平衡。
这两种功能使得蝙蝠算法能够在算法优化的初始阶段,获得好的结果。 但是,与其他智能算法一样,蝙蝠算法也存在收敛速度慢,易于收敛到局部极值点以及应用领域有待进一步扩大等问题。
蝙蝠算法的应用与发展现状
本论文从蝙蝠算法的收敛性分析、蝙蝠算法在连续域函数优化问题中的应用以及蝙蝠算法在离散域函数优化问题中的应用等三个大的方面进行了深入研究。主要研究工作包括:
(1)总结了蝙蝠算法的研究现状,简要介绍了蝙蝠算法的基本原理,总结了几种蝙蝠算法的当前版本,总结了目前蝙蝠算法的应用领域,表明蝙蝠算法往往比其他算法更先进、运用更广泛。类似算法和未来研究前景的三个主要原因。
(2)将蝙蝠算法简化为一维单蝙蝠,定义速度和位置更新两种模式,并利用特征方程分析该方法的收敛性。发现模式2优于模式1收敛。同时,给出了该模型。2中的参数选择方法,并通过数值模拟实验验证了相关分析的正确性。
(3)利用量子比特对蝙蝠的位置进行编码,利用量子旋转门寻找蝙蝠的最佳位置,利用量子非门实现蝙蝠变异,避免早熟收敛和峰值函数。优化问题用典型的复杂函数进行测试,并与其他算法进行比较。结果表明,该算法能有效避免局部优化,具有较强的全局优化能力。
(4)用和声搜索算法进行全局搜索,用差分进化算法来进行局部搜索,提出混合算法来解决多目标优化问题。实验结果显示:该算法在收敛性指标上比其他算法具有一定的优越性。
和声搜索算法,渐进式全局搜索,差分进化算法,前向局部搜索,蝙蝠算术基本框架组合平衡所有位置搜索和局部部分搜索。混合算术解决多目标规划问题,具有高效结果性、收敛速度有很强的优势等特点。
(5)将蝙蝠算法与原始混合遗传算法和二进制蝙蝠算法相结合,提出了0-1背包问题的遗传变异蝙蝠算法和0-1背包问题的二进制蝙蝠算法。实验结果显示:上述算法具有一定的寻优性能,比用来比较的其他算法具有更好的收敛性。
(6)重新定义蝙蝠算法的相关算子,设计一种蝙蝠算法来解决旅行商问题和最小比率旅行商问题[1],利用2-opt来局部优化旅行商问题,用城市子排列逆序策略来局部优化最小比例旅行商问题。实验结果表明:上述算法不仅可以有效解决该问题,并且比其他算法具有更好的搜索性能。整篇论文对蝙蝠算法的收敛性和应用性进行了较为全面的分析和研究,最后总结所做的工作。
0-1背包问题的来源及求解应用
背包问题[3](KP)最早是由Dantzing在20世纪50年代提出和研究的,它是运筹学中一个典型的组合优化问题和NP完全问题。0-1背包问题可以应用于预算控制,货物装载,投资决策,项目选择等。解决背包问题仍然是一个需要解决和改进的问题。解决0-1背包问题具有经济性,方便性,科学性和灵活性的显著特点。
解决背包问题的关键在于算法的收敛能力和优化能力,精确的算法主要包括枚举法,分支定界法,动态规划法和回溯法。这些算法的时间复杂度将随着物品的数量和背包的容量而增加,扩展的指数增长导致应用范围有限。
背包问题可以分为两类:物体可以分割的背包问题和物体不可分割的背包问题。在实际问题中,决策项目往往要求物体不可分割,即0-1背包问题。近年来,智能算法不断成熟,如蜂群算法、蚁群算法、遗传算法、粒子群算法、萤火虫算法、模拟退火算法、猴群算法、细菌觅食优化算法、人工杂草优化算法、文化算法、和谐搜索算法、狩猎搜索算法和声搜索算法等。它们不用依赖于梯度信息,在0-1背包问题求解中体现了其性能的优异,但仍存在稳定性差、成功率低等难题。
1.3 问题描述
背包问题是一个常见的组合优化问题,可以表示为:物品的数量是m,第i个物品的体积(重量)和价值分别是wi和p,一个背包的最大容量(可以装载的最大重量)为C,找出一种包装方法,使得如果装载物品的体积(重量)不超过背包的最大容量(最大值)装载物品的总值最高可以承受的重量。假设W={w1,w2,···,wn}表示体积(重量)向量,P={p1,p2,···,pn}表示价值向量,则0-1背包问题模型可以表示为(1.1)所示:
| (1.1) |
其中xi为二值决策变量:xi=0表示相应的(第i个)物品没有装人背包中,xi=1表示相应的(第i个)物品装人了背包中。
从上述描述可以看出,求解0-1背包问题的解的实质是确定解向量X={x1,x2,···,xn}中每个组件xi(0或1)的值总共有2n个可能的值。 因此,在大规模的情况下,确切的方法是不可取的。
背包问题属于约束条件下的离散优化问题,在使用二进制算法求解时,需要对模型进行变换。惩罚系数被引入来对不可行的解决方案施加惩罚。最终转化如式(1.2)所示。
| (1.2) |
其中:λ为惩罚系数,是一足够大的数。
蝙蝠算法及其应用
众所周知,蝙蝠靠声呐回声定位来捕食与飞行,而回声定位主要由它们发出的脉冲的速度V、响度D和频率来决定,所有蝙蝠利用这种感知能辨别与物体之间的距离和形状,波长与寻找猎物的蝙蝠的大小相似,并且当接近物体时声学响度将被最小化。
2.1 蝙蝠算法的原理
我们设在d维搜索空间下,第i只蝙蝠在t时刻时的位置为Xit,速度为Vit,那么可以推出相应的t 1时刻的位置和速度分别是Xit 1和Vit 1,其更新公式如(2.1)、(2.2)、(2.3)所示:
| (2.1) |
| (2.2) |
| (2.3) |
其中 表示随机向量,Fi是第i只蝙蝠的声波频率,Fmin、Fmax分别表示蝙蝠中的最小、最大频率, 是局部最优解,作为 、 的产品代表,所以速度增加,可以通过改变 或 来改变速度,针对每个新解决方案可以通过以下(2.4)方式使用随机搜索得到:






| (2.4) |
其中 是一个随机数, 是平均响度。
是一个随机数, 是平均响度。

2.2 响度与脉冲速度
达到目标后,响度D(i)减少而脉冲发射率V(i)增加,所以当响度达到最低的时候(0)就意味着找到了物体,蝙蝠的响度更新方式如(2.5)所示:
| (2.5) |
随着时间接近无穷大,实现零响度[2],并且 ,对于蝙蝠算法相应的伪代码[18]如下:

蝙蝠算法的伪代码: |
Define the objective function f(x), X = (x1, x2,...,xd); Initialize bat population with their position (xi) and velocity (vi) where i = 1, 2,...n; Set initial pulse frequency (fi) where fi ∈ [fmin, fmax] Initialize pulse rate (vi) and loudness (Di); Assign boundaries for each parameter; begin while (t lt; maximum number of iterations(tmax)); Generate new solutions by adjusting frequency and updating velocities amp; loudness; if (rand gt; vi) Choose a best solution among the best solutions; Select a best solution among the generated solutions amp; obtain a local best solution around the selected best solution by a local random walk; end if if (rand lt; Diamp;f(xi) lt; f(x∗)) Obtain new solutions with increasing pulse rate (vi) and reducing loudness (Di); end if Order bats according to the obtained solution and choose current best (x∗); end while Obtain the best solution end |
和现存的其他算法相比较,蝙蝠算法有以下两个优势:(1)良好的协调频率的能力;(2)条件满足时全局搜索与局部搜索的转化。
2.3 数值仿真
为了更好的比较蝙蝠算法的寻优能力,构造了速度变化的两个公式(2.6)、(2.7):
| (2.6) |
| (2.7) |
式(2.2)、(2.3)体现了算法的全局搜索能力,而(2.6)、(2.7)是蝙蝠算法的两种不同速度构造。这里可以看出式(2.2)是式(2.7)的一种特殊情况,即当ω≡1时,把(2.6)与(2.3)的结合情况定义为模式一,把(2.7)与(2.3)的结合情况定义为模式二。
2.4 函数测试
采用四类常规的测试函数
- Sphere模型:
| (2.8) |
其中-100≤xi≤100,min(f1)=f1(0,0,···,0)=0
- Schwefel函数2.21:
| (2.9) |
其中-100≤xi≤100,min(f2)=f2(0,0,···,0)=0
- Schwefel函数1.2:
| (2.10) |
其中-100≤xi≤100,min(f3)=f3(0,0,···,0)=0
(4)Step方程:
| (2.11) |
其中-100≤xi≤100,min(f4)=f4(0,0,···,0)=0