几种智能算法的改进及其在航迹规划建模中的应用开题报告
2020-02-20 09:59:49
1. 研究目的与意义(文献综述)
无人机(unmanned aerial vehicle,简称uav)是利用自备的程序控制装置和无线电遥控设备操纵的不载人飞机。 相较于有人驾驶飞机,无人机具有造价低廉,体积小,使用便捷,航行环境要求低,无需考虑人的承受状态,在作战时生存能力更强等特点。基于以上优点,无人机在军用和民用两个方面的应用前景都十分广泛。民用方面,在航拍、微型拍摄、灾难救援、快递运输、传染病的监控、电力巡检、影视拍摄等领域都有非常重要的应用;军事方面,随着无人机技术的发展,其正在影响着当前的空战格局,对未来的空战和制空权有着重要的意义。无人机航迹规划是指在一定的约束条件限制下,按照某种评价标准寻找起点到目标点的最优路径。[1]航迹规划问题是当今无人机设计中十分重要的问题,其最为核心的内容是航迹规划算法,国内外专家和学者们经过长期的研究,开发出的具有代表性的航迹优化数值方法有:直接法、直接打靶法、多重直接打靶法、配置发、微分包含法、间接法、动态规划法、快速探索随机树法、遗传算法和蚁群算法以及粒子群算法。
遗传算法(genetic algorithm,ga)是一种模拟自然选择和遗传机制的不依靠梯度信息的智能全局优化算法,具有较强的鲁棒性,对初值不敏感,对于一些大型、复杂非线性系统的全局优化问题表现出良好的性能,遗传算法是建立在自然选择和群众遗传学机理基础上的,具有广泛适应性的搜索方法。[2]它是在1975年被美国的j.holland教授率先提出的,具有直接对结构对象进行操作,不被函数的连续性和求导限定的特点;具有较好的全局寻优能力和隐并行性;采取了概率化的寻优方法,能够自适应地调整搜索的方向。遗传算法的这些优良的特点,逐渐被人们广泛地应用于信号处理、自适应控制和机器学习等领域。
蚁群算法(ant colony optimization,aco)是一种用来寻找优化路径的启发式算法。它由marco dorigo于1992年在他的博士论文中提出,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为[3]。蚁群算法是以蚂蚁群体的觅食行为和觅食策略为基础开发出的新的智能仿生算法,蚂蚁的爬行路线代表了求解问题的初始解,对所求问题的数学表达式的具体描述的依赖性弱,且对全局最优解的优化能力很强。蚂蚁算法具有正反馈、较强的鲁棒性、优良的分布式并行计算机制、易于与其他方法相结合等诸多优点,但同时也存在着搜索时间过长、容易陷入局部最优化、收敛速度慢等缺陷。[4]
2. 研究的基本内容与方案
2.1研究的基本内容和目标
本文将要研究的无人机航迹优化为飞行路径中的威胁规避问题。具体问题如下:
位于P点(该点坐标为(0,100))的某无人机基地配备有若干架无人机组成的支援部队,当前该无人机编队将前往目标点S(该点坐标为(300,100))执行支援补给的任务,航行过程中无人机编队需要规避掉A01~A07各种型号雷达的监控范围(各个雷达的具体坐标和监测半径见表1),并且以最优最快的路径到达目标点S。
| 点位名称 | 雷达坐标 | 监测半径 | 点位名称 | 雷达坐标 | 监测半径 |
| A01 | (50,100) | 25 | A05 | (160,80) | 20 |
| A02 | (100,80) | 15 | A06 | (220,120) | 25 |
| A03 | (120,160) | 20 | A07 | (260,110) | 10 |
| A04 | (180,140) | 30 |
|
|
|
表 1
将上述问题中的各个点的坐标转化成平面示意图如下:
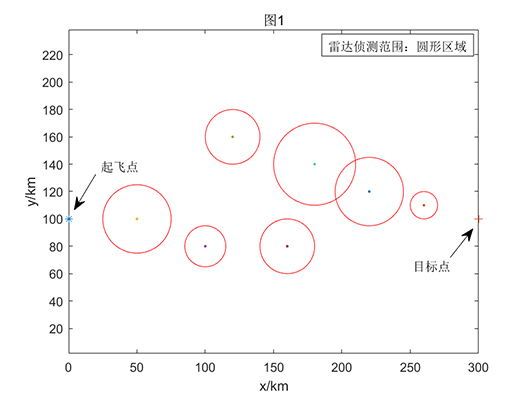
本文的主要目标是基于最优化理论对无人机的轨迹进行建模优化和分析,规划出一条从基地起飞,并规避掉航行过程中A01~A07各雷达的圆形监测范围,到达目标点的最优最短路径。
2.2拟采用的技术方案和措施
无人机路径规划问题本质上是数学中在有限条件下获得最优成本值的一个优化问题,在数值方法中通常被建模为一个非线性最优控制问题。[6]建立无人机航迹规划的最优控制问题模型如下:
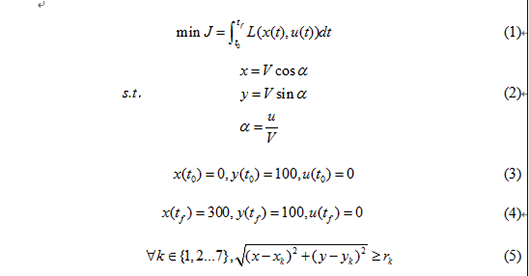
其中t(0)和t(f)分别为初始时刻和最终时刻,x和y分别为的无人机横纵坐标,u和V分别为无人机的法向加速度和速度,依据无人机运动方程,可计算无人机飞行角度a。k为威胁雷达的编号,(x(k),y(k))为威胁雷达的坐标,r(k)表示编号为k的雷达的监测半径。L为代价函数。上述(1)式为目标函数,其极值点为整个航迹的代价之和最优解,(2)式为无人机等高匀速飞行的运动方程,(3)和(4)分别为初始时刻和最终时刻的无人机坐标和法向加速度的等式约束条件。(5)式为无人机航迹规避威胁雷达监测的不等式约束条件。
对于该优化模型有很多求解方法,本文将采用的是之前详细介绍的遗传算法,蚁群算法和粒子群算法三种启发型智能算法,并通过编程语言实现,求出此问题的最优解的近似解,比较三种种算法的优劣,结合学过的最优化理论知识对相应算法进行改进优化,从而模拟出上述无人机航迹规划问题的最优策略。
3. 研究计划与安排
1-3周:查阅文献,完成开题报告
4-6周:完成论文综述,查阅无人机航迹规划问题的各种模型的建模方法和优化算法
7-10周:学习航迹规划的各种算法,重点学习遗传算法,蚁群算法和粒子群算法
11-13周:完成无人机航迹规划问题的遗传算法,蚁群算法和粒子群算法的c语言和matlab仿真实现,比较三种算法的优劣,并进行相应的改进,规划出最优执行方案
14-15周:完成论文写作及外文翻译,准备答辩
4. 参考文献(12篇以上)
[1]李晓萌,王道波,郭继凯,杨华,王博航.基于某种生物启发式算法的无人机航迹规划[J].机械与电子,2018,36(11):15-19.
[2] 黄国强,陆宇平,南英.飞行器轨迹优化数值算法综述[J].中国科学:技术科学,2012,42(09):1016-1036.
[3] 耿振余,陈治湘,黄路炜,李德龙,刘思彤,周宏升,王立华编著.软计算方法及其军事应用[M];国防工业出版社,2015.12.
[4] 古明家. 蚁群算法优化策略及其应用[D].广西民族大学,2009.
[5] 张利彪,周春光,马铭,刘小华.基于粒子群算法求解多目标优化问题[J].计算机研究与发展,2004(07):1286-1291.
[6] Zhang Z , Li J , Wang J . Sequential convex programming for nonlinear optimal control problems in UAV path planning[J]. Aerospace Science and Technology, 2018, 76:280-290.
[7] 王庆贺. 基于最优化理论的三维多无人机协同任务规划技术研究[D].解放军信息工程大学,2017.
[8] 张殿富, 刘福, 杨俊. 基于多级优化的粒子群算法在航迹规划中的应用[J]. 海军航空工程学院学报,2013,28(1):1673-1522.
[9] 杨雅宁, 蔺勇. 基于蚁群算法的一种无人机二维航迹规划方法研究[J]. 电脑知识与技术, 2016,12(28):189-191.
[10] 邵长旭,王茂森,戴劲松,陈斌.基于蚁群算法的无人机最短航路规划[J].兵工自动化,2018,37(09):93-96.
[11] 王琼,刘美万,任伟建,王天任.无人机航迹规划常用算法综述[J].吉林大学学报(信息科学版),2019,37(01):58-67.
[12] 曹良秋,吴立巍.基于遗传算法的无人机航路规划研究[J].科技创新与应用,2018(24):27-30.
[13] 王钦钊,程金勇,李小龙.多无人机协同任务规划方法[J].火力与指挥控制,2018,43(03):86-89 94.
[14] 李华伟. 多无人机协同任务规划研究与实现[D].西安电子科技大学,2014.
[15] 王祝,刘莉,龙腾,温永禄.基于罚函数序列凸规划的多无人机轨迹规划[J].航空学报,2016,37(10):3149-3158.
[16]过娟,褚晶,闫杰.基于控制向量参数化和迭代凸规划的无人机编队飞行的建立[J].西北工业大学学报,2016,34(04):607-613.
[17] 王希彬,宋广大,杨飞.基于最优控制的无人机主动SLAM航迹规划[J].兵工自动化,2018,37(12):55-57.
[18] 辛贵州. 无人飞行器航迹规划算法研究[D].哈尔滨工程大学,2010.
[19] 巴海涛. 无人机航迹规划研究[D].西北工业大学,2006.
[20]Semyon M , Kabamba P T , Zeitz I F H . Optimal UCAV path planning under missile threats[J]. 2005.
[21] Sicong Li,Chao Deng,Ruizhi Sun,Qiannan Wu,Kaiyi Zhao,Multi-path intelligent planning method based on grid division and value calculation, IFAC PapersOnLine 51-17 (2018) 179–184.
[22] Veldhuizen, David A. Van, Lamont, Gary B. Multiobjective Evolutionary Algorithms Analyzing the State-of-the-Art. Evolutionary Computation, 2000, 8(2):125-147.
[23]Maulik U , Bandyopadhyay S , Mukhopadhyay A . Genetic Algorithms and Multiobjective Optimization[M]// Multiobjective Genetic Algorithms for Clustering. Springer Berlin Heidelberg, 2011.
[24] Chingiz H, Sitki Y.LQR Controller with Kalman Estimator Applied to UAV Longitudinal Dynamics. Positioning, 2013,4:36-41.




