英语原文共 10 页，剩余内容已隐藏，支付完成后下载完整资料

---

在这个课程中，我们会探讨被称为格的数学对象。格是什么？如图1所示，这是一个周期性结构在n维空间中的点的集合。三维格天然存在于晶体中，就像堆积的橘子。从历史上看，格从18世纪后期就被数学家研究，如拉格朗日，高斯，以及后来的闵可夫斯基。

表1：二维格

最近，格已成为计算机科学的一个活跃的研究课题。它们被用作一个算法工具来解决多种问题;它们在加密和密码分析中拥有很多应用；并且从一个计算复杂点来看，它们具有一些独特的性能。这些都是我们将在这个课程中看到的主题。

1 格

我们从一个格更正式的定义开始探讨。

定义 1 (格) 给定N个线性无关的向量 ，由它们产生的格被定义为

我们指定为格的一组基。同样地，如果我们把B定义为以为列的阶矩阵，那么，由B生成的格表示为

我们可以得到这个格的秩是n，维度是m。如果n＝m，那么这个格被称为满秩格。在这门课中，我们通常会把满秩格视为更一般的情况，而不是本质上的不同。

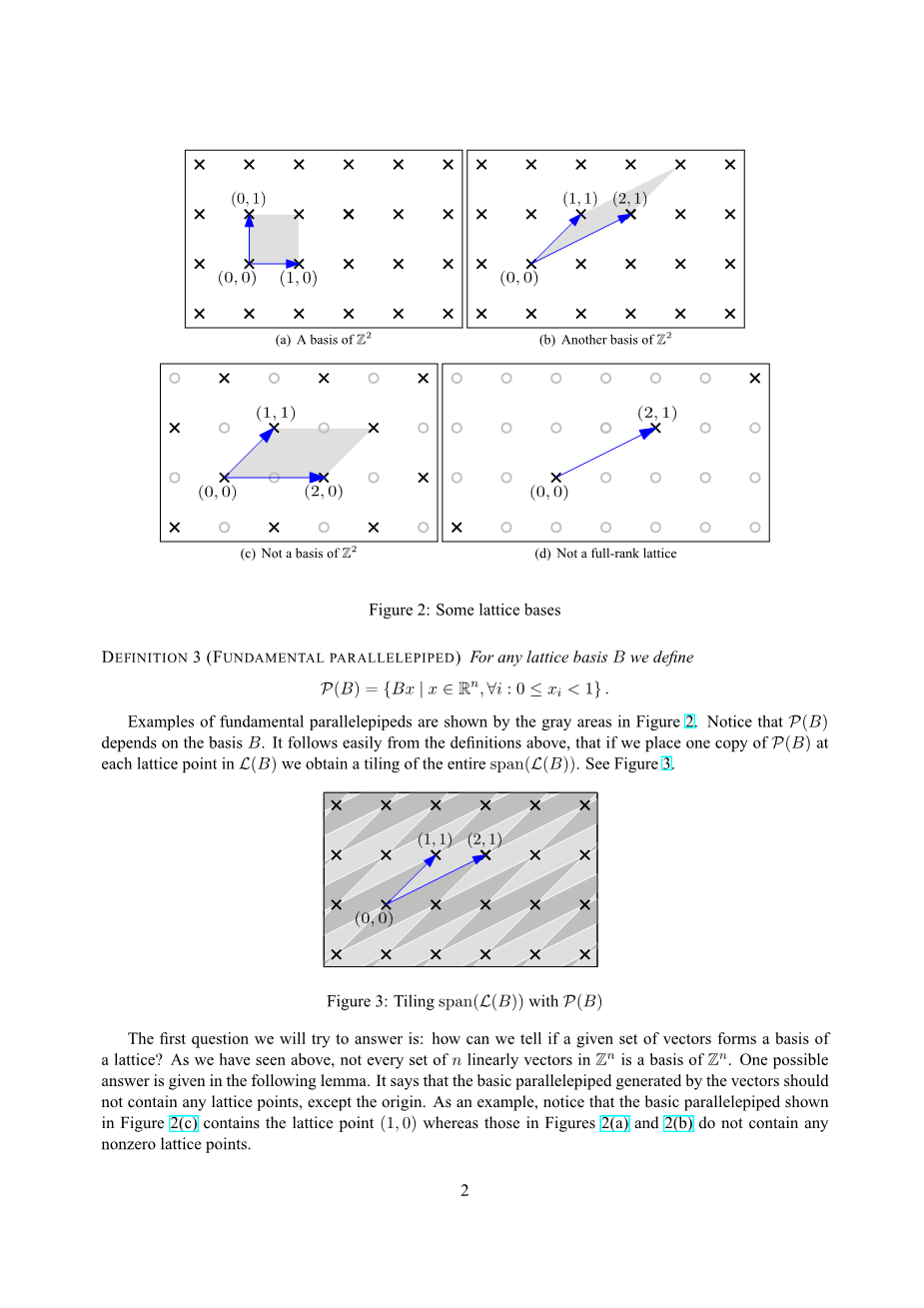
让我们看下面的一些例子。由向量和形成的格叫做，一种包括所有整数点的格（见图2（a））。这个基不是唯一的：向量和也能生成（见图2（b））。然而的另一组基是由向量和给出的。另一方面，向量和不是的一组基：代替地，它生成坐标之和为偶数的所有整数点的格（见表2（c））。我们上述的这些例子都是关于满秩格的。一个非满秩格的例子是L（）（见表2（d））。它的维度是2，秩是1。最后，格 Z=L（（1））是一个一维满秩格。

1. 的一组基

（b）的另一组基

（c）不是的一组基

（d）非满秩格

图 2: 一些格的基

定义 2 (跨度) 格的跨度L(B)就是由组成它的向量扩张而成的线性空间，

定义3（基本平行六面体）对于任意格的基B，我们定义

图2中灰色部分展示的就是基本平行六面体的例子。值得注意的是，P（B）取决于基B。通过上面的定义，我们能够很容易得知，如果我们将P（B）复制到L（B）中的每一个格点上，我们将得到整个span(L(B))的平铺。见图3。

图3：用P（B）来平铺span（L(B)）

我们会尽力回答的第一个问题是：我们如何判断一组给定的向量是否组成一个格的一组基？正如我们上面看到的，不是中的每一组n维向量都构成的一组基。一个可能的答案在下面的引理给出。它指出，一个由向量生成的基本平行六面体，不应该包含任何原点以外的格点。作为一个例子，请注意，图2（c）中所示的基本平行六面体包含着格点（1,0）而在图2（a）和2（b）的基本平行六面体却不包含任何非零格点。

引理 1 假设是一个秩为n的格，是n个线性无关的格矢。那么组成的一组基当且仅当.

证明： 首先证明充分性，假设组成的一组基。那么根据定义，是关于它们所有的以整数为组合系数的线性组合的集合。又因为定义为的组合系数在[0,1)上的线性组合的集合，所以2个集合的交集是{0}.

再证明必要性。假设，因为为n秩格，线性无关，那么对于任意的格矢，必定能表示成，其中.又因为根据定义，格对于加法是封闭的，因此向量也在中。通过我们的假设，xrsquo;=0.这意味着，所有的都是整数，因此x是以整数为组合系数的线性组合。

□

我们需要解决的第二个问题就是如何确定2个给定的基是否等价，即生成同一个格（用公示表示，就是）.对于这一点，我们需要引入下面的定义。

定义4 （单模矩阵）一个矩阵被称为单模矩阵，如果。

例如，矩阵就是单模矩阵。下面的引理出现在作业中。它告诉我们，一个单模矩阵的逆仍然是单模矩阵(所以它遵循，单模矩阵的集合关于矩阵的乘法作成一个群)。

引理2 如果是单模矩阵，那么也是单模矩阵，并且.

引理3 两组基是等价的，当且仅当，其中为任意单模矩阵。

证明：先证明充分性。假设，因此对于中的任意n列，都有。这意味着存在一个整数矩阵使得。同理，也存在一个使得。于是有，所以我们得到

考虑到这个因素，我们得到，于是有。又因为U,V都是整数矩阵，这意味着。

再证明必要性.假设，其中为单模矩阵，因此中的每一列都包含于，于是我们得到.此外，有。既然为单模矩阵（引理2），我们同样能得到.于是，有.□

作为一个直接推论，我们得到，是的一组基，当且仅当它是单模矩阵（可以通过图2中的例子验证这一点）。

另一种验证两组基是否等价的方法，将会出现在作业的引理中。

引理4 两组基等价当且仅当其中一个可以通过下面的列变换：

我们需要的最后一个基本概念如下。

定义5（行列式） 令为一个n秩格。我们这样定义的行列式，用表示的n维体积。在符号上，可以写成。在是一个满秩晶格的情况下，B是一个方阵，并且有.

在晶格的行列式被明确定义的情况下，它是独立于我们对基B的选择的。的确，如果和是的两组基，那么根据引理3，就有，其中为单模矩阵。因此，

晶格的行列式与其密度成反比：晶格的行列式越小，晶格的密度就越大。用更精准的术语来说，如果有一个大球K（在的跨度范围内），随着K的大小趋于无穷，K内部的格点数量将要无限接近.

2施密特正交

施密特正交是线性代数中通过n个线性无关向量创建一组n个正交向量的基本过程。它的工作原理是让每个空间向量正交于前一个向量的跨度。详情看图4的图示。

图4：格莱姆-施密特正交化

定义6 对于n个线性无关的向量，我们定义他们的格莱姆施密特正交化为根据下面的式子

，其中

得到的向量序列.显而易见，是中与正交的组成部分。

我们现在来说说有关施密特正交化的一些基本且易于验证的属性。首先，顾名思义，对于任意的，都有。第二，对于所有，都有span()=span().第三，向量组不必是的一组基。事实上，他们通常甚至不在那个格内（见图4）。最后，向量的顺序也至关重要：这就是为什么我们认为他们作为一个序列，而不是作为一组。

下面是一个格拉姆施密特方法的有效的应用。假设是中的n个线性无关的向量组并且考虑通过得到的正交基。在此基础上，向量组作为阶矩阵的列被给出。

在m=n的情况下，这是一个上三角方阵。通过这种表示方式，很容易看出，，或等同地，，都可以由给出。事实上，这种相等可以看作式的n维扩展计算平行四边形的面积。

3 连续极小

晶格中的一个基本参数是最短非零矢量的晶格长度（因为零向量总是包含在一个格及其规范为零，所以我们不得不要求一个非零向量）。这个参数用表示。这里的长度用的是欧几里得范，或者说范，定位为。我们通常用指代这一范。偶尔在这个过程中，我们也考虑其他范，例如范，，或者范，。

定义的等效方式如下：跨越维1空间的包含所有格点的球的半径r的最小值。这个定义导致了以下被称为连续极小的概括。见图5.

定义7 假设是一个n秩格。对于，我们定义第i个连续最小为

其中，是一个围绕0半径为r的封闭球。

图5：

以下定理给出了以格子的最短非零向量的长度的一个有效下限。

定理5 假设B是n秩格的一组基，是它的施密特正交，那么有

证明：令为任意非零整数向量，并且让我们表明。令取得最大值，使。于是有

其中对于所有，都有，并且。另一方面，，因此我们推断

□

定理1的另一种证明如下。在正交基中，晶格由（5）式中的矩阵的列的所有整数的组合给出。很容易看出，在任何这样的非零组合中，最底层的坐标至少是在绝对值上的最小值。

推论6 是一个格，存在，使得任意2个不相等的格点都有。

证明：对于任意不等的，向量x-y是中的非零向量。因此，通过定理5有

要求7 晶格的连续最小值得以实现，即对于每个，都有向量满足.

证明：通过推论6，半径为的圆仅仅包含有限多个格点。遵循的定义，这些向量中必须有一个长度为.□

3.1 连续极小的上限

我们现在在连续极小的基础上提出闵可夫斯基上限。为简单起见，在本节中，我们只考虑满秩格；想扩展到非满秩格是非常容易的。我们从Blichfeld定理开始。

定理8（BLICHFELD）对于任意满秩格和可测集（其中），存在2个不等点使得.

图6：Blichfeldt定理

证明：B是的一组基，当x在之外，集合形成的一个分区。现在定义（见图6）.由于，我们得到结论.定义，可得，我们最后可得：

因此，必然存在,,使得empty;.令z为中一点，则z x属于，z y属于，并且(z x)-(z y)=x-y属于.

通过Blichfeld定理的推论，我们可以得到下面由闵可夫斯基推导出来的定理.它规定，任何足够大的中心对称凸集包含一个非零格点。集合S中心对称，如果对于任意都有

.它是凸集，如果对于任意和任意可得.很容易看出，如果我们丢掉关于S的这两个要求中的任意一个，那么这个定理就不成立了.

定理9 (MINKOWSKI凸体定理)假设为一个秩为n的满秩格，那么对于任意的中心对称凸集S，如果，则S包含一个非零格点.

证明：定义,于是有.通过定理8，存在2个点使得为一个非零格点.通过定义，有，又因为S中心对称，可得.最后，由于S是凸集，则有也属于S.见图7.

图7：MINKOWSKI凸体定理

要求1 半径为r的n维球的体积是.

证明：在此之前，因为这个球中包含着一个边长为的立方体，则有

□

我们现在在最短非零向量的长度上得到了下界.

推论2（闵可夫斯基第一定理）对于任意秩为n的满秩格，都有

证明：按定义，（开）球中没有非零格点.根据定理9和要求1，可得

通过重新排列，我们得到了的下界.□

术语或许看起来有点怪，但是实际上是很自然的：它可以确保表达扩展正常.事实上，考虑到晶格是由扩大c倍所得，那么就有.另外，所以右手侧也按照预期地扩大c倍.因此，我们可以这样等价陈述闵可夫斯基的第一定理：任意行列式等于1的n秩格包含一个长度不超过的非零格点.

这是多么紧的约束？很容易看出，还有一些（约束）不这么紧的例子.例如，由向量形成的晶格（＞0且极小），其行列式为1,但其非零向量的最短长度为.另一方面，考虑晶格，它的行列式为1而，所以限制更紧，但实际上仍然不算紧.实际上，总所周知，对于任意n，存在一个行列式为1的n秩格，其最短非零向量的长度至少为,c为一常数.所以上升到一个常数，闵可夫斯基给出的限制很紧.实际上，通过一个略微更小心的分析，我们可以把提高到,c为一常数.

最后，我们提到，在上面的讨论中我们也可以考虑范.很简单就可以把闵可夫斯基定理扩展到别的范.所需要的只是计算在被给范下的球的体积.

闵可夫斯基第一定理讨论了最短非零向量，即第一个连续最小值.这个限制的加强由闵可夫斯基第二定理给出.代替仅仅考虑，这个限制考虑了所有的几何平均值（显然不小于）.

定理3 (MINKOWSKI第二定理)对于任一秩为n的满秩格，都有

证明：令为实现连续极小的线性无关向量组，.令是它们的斯密特正交基.考虑轴为，长度为的开椭球，则有

见图8.

图8：椭球T.向量在T的边界上，在T的严格外.

我们要求，T不包含任何非零晶格点.确实，对于任意非零，取满足的最小值，必然有,否则会变成长度小于的线性无关向量组.现在有

并且因此.

根据闵可夫斯基凸体定理，.但是在另一方面，

结合2个限制，我们得到

□

4计算问题

闵可夫斯基第一定理指出，任意n秩格包含一个长度不超过的非零向量.然而，它的证明并没有建设性：它并没有给出一个算法让我们找到这样的晶格向量.事实上，没有已知有效的算法能找到这样短向量.

为了讨论这样的计算问题，让我们定义涉及格的最基本的计算问题：最短向量问题，或简称SVP.在这里，我们给出了一个格，我们应该找到最短的非零格点.更确切地说，这里是SVP的三个变种，取决于我们是否必须找到最短向量，求出它的长度，或者仅

剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[146342]，资料为PDF文档或Word文档，PDF文档可免费转换为Word