一维磁流体力学方程组解的存在性开题报告
2020-04-10 16:01:58
1. 研究目的与意义(文献综述)
磁流体力学(mhd)是关于电磁场中导电流体的一门学科,mhd中所研究的液态金属到等离子体,在物理学领域内都有广泛应用。[1] 磁流体力学包括磁流体静力学和磁流体动力学。磁流体静力学研究导电流体在电磁力作用下的静平衡问题,如太阳黑子理论、受控热核聚变的磁约束机制等。磁流体动力学研究导电流体与电磁场相互作用时的运动规律,如各种磁流体动力学流动和磁流体动力学波等。但磁流体力学通常即指磁流体动力学,而磁流体静力学被看作磁流体动力学的特殊情形。
mhd偏微分方程组描述了导电流体在电磁场中的运动状态, 由于其重要的物理应用背景,mhd方程组引起了广大物理学家、应用数学家的研究兴趣,也取得了丰富的研究成果,特别是不可压缩mhd方程组。近年来,随着科学技术和理论分析工具的进一步发展,可压缩mhd方程组受到越来越多的关注。但是,相比较不可压缩方程组,可压缩mhd方程组在其物理机制和数学结构上更加复杂,无论是在技巧方法还是分析工具等方面都与不可压情形有很大的不同。[2]
在本次研究中,我们仅考虑一维的情形。
2. 研究的基本内容与方案
三大守恒定律并电磁效应,可以导出磁流体力学方程组的模型。但是约束条件越少的方程组,实际上越复杂,在选取方程的时候考虑到这一点,本次论文最终采用了,欧拉坐标下,无粘无外力的一维可压缩等熵的mhd方程组:
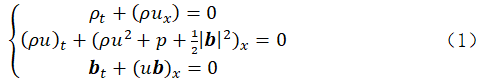

3. 研究计划与安排
第一周:相关模型文献综述,求解特征向量。
第二周:利用上周查到的方法进行试求解,并继续查找文献。
4. 参考文献(12篇以上)
[1] chen g q, wang d. global solutions ofnonlinear magnetohydrodynamics with large initial data[j]. journal ofdifferential equations, 2002, 182(2):344-376.
[2] 张剑文. 关于可压缩mhd方程组的若干研究进展[j]. 厦门大学学报(自然版), 2011, 50(2):175-186.




