1. 研究目的与意义（文献综述）

欧拉-泊松方程组主要研究受到电场外力或自引力作用的流体的运动。在流体动力学模型中，欧拉-泊松方程组描述半导体或等离子体中电子的运动；在生物学模型中，可以描述蛋白质通道中离子的传输，即离子在细胞外部和薄膜的细胞质边之间的传动^[1]。文献[2][6]指出如果方程的初始数据在次临界区域内选取时可以得到整体光滑解。如果初始数据超出次临界区域，文献[2]给出了这种情况下解会在有限时间内分解的例子，证明了欧拉-泊松方程组临界阈值的存在性，文献[3]通过研究热扩散效应、阻尼松弛和电势对可压缩欧拉-泊松方程的大时间行为的耦合效应，表明了这种耦合效应不够强到足以阻止奇异性的形成以及激波的产生。因此，考虑欧拉-泊松方程组的弱熵解的存在性和大时间行为有着很重要的意义。文献[4-5][12-13]证明了整体弱熵解的存在。文献[4]研究了半导体水动力模型的柯西问题，利用分步Lax-Friedrichs函数和Godounov方案，得到了具有大初始数据的整体弱解的存在性定理。文献[5]根据Nishida利用Glimm函数构造的具有任意大数据的欧拉系统的整体弱解，再考虑电荷准守恒定律对电场总变化的一致估计，证明了一维欧拉-泊松系统的解的全局存在性。文献[6-7]假设初始数据是漂移扩散方程的稳态解的扰动，利用系统的等价形式，证明由此产生的进化解在时间上渐近收敛到未受干扰的状态。为了克服系统的非线性共振和源项的非局部行为的困难，文献[8]利用了一种冲击捕获数值方案，用补偿紧性证明了该方程的冲击捕获方案的收敛性和一致性，证明了整体弱熵解的存在性。对于二维欧拉-泊松系统在缓慢分散线性流和某些非局部非线性共振障碍上的困难，文献[9]提出了一种新的方法克服了这些困难，证明了整体解的存在性。文献[10]克服了由于耦合项造成的困难，提出一种一致估计方法，证明了任意大初始数据整体弱熵解的存在性。文献[14-15]分别给出了小初值光滑解和分片光滑解的大时间行为。文献[11]给出了整体弱熵解的大时间行为，利用系统的等价形式和熵耗散的性质，证明在背景电流充分小时，一致有界的弱熵解将随着时间t指数衰减到稳态解。

2. 研究的基本内容与方案

本文考虑如下的欧拉-泊松方程组：

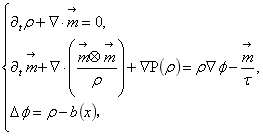
3. 研究计划与安排

1-3周：查阅文献，完成开题报告

4-6周：根据参考文献尝试进行简单的计算

7-10周：在原问题上进行创新，计算

4. 参考文献（12篇以上）

[1] chen d p, eisenberg r s, jerome j w, et al. hydrodynamic model of temperature change in open ionic channels.[j]. biophysical journal, 1995, 69(6):2304.

[2] tadmor e, wei d. on the global regularity of sub-critical euler-poisson equations with pressure[j]. journal of the european mathematical society, 2006, 10(3):págs. 757-769.

[3] wang d, chen g q. formation of singularities in compressible euler–poisson fluids with heat diffusion and damping relaxation[j]. journal of differential equations, 1998, 144(1):44-65.g