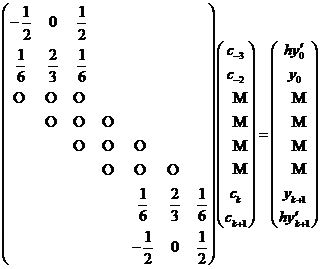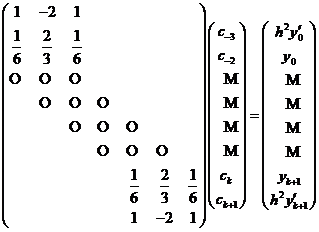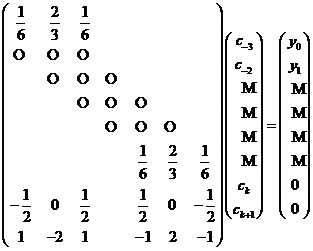摘 要

样条函数是一种由分段多项式定义的函数，由于其良好的性质，被广泛应用到各个领域中，具有重大的实用价值。

本文前半部分从多项式样条函数空间出发，介绍B样条函数，然后利用B样条函数构成一组具有局部支撑性和对称性的基，最后利用B样条函数表示三次样条插值函数，并写出系数矩阵。

本文后半部分从三个方面阐述了样条函数的应用。首先，我们利用B样条函数求函数的数值微商和数值积分，与传统的数值方法进行了比较。其次，我们根据B样条函数求解常微分方程初值问题，推导出一个隐式格式，此隐式格式稳定且局部截断误差为O(h⁵)，整体截断误差为O(h⁴)。由于隐式格式不便计算，所以我们使用欧拉预测-校正法对此格式进行改进，得到了一个便于计算的格式，且其局部截断误差至少为O(h⁴)，并将此格式与欧拉预测-校正方法以及四阶龙格库塔方法进行比较，所得结果较为满意。然后，我们利用B样条函数对一组数据进行最小二乘拟合，将其与多项式最小二乘法进行比较，拟合结果表明利用B样条函数作为基函数的拟合效果更好。最后，我们分析了B样条函数的节点个数和次数对拟合结果的影响。结果表明，固定次数时，随着节点个数越多，拟合效果越好，但计算量不断增加，均方误差减小速度逐渐变缓；固定节点个数时，随着次数的增加，计算量不断增加，其均方误差整体有逐渐增大的趋势，但都在同一个数量级上，可以满足所需要的精度。因此，结合二者分析，在实际情况中，我们可以选取合适的节点个数和次数来快速地达到较好的拟合结果。

关键词：B样条函数；数值微商；数值积分；常微分方程；最小二乘法

Abstract

Spline function is a function defined by piecewise polynomials. Because of its good properties, it is widely used in various fields and has great practical value.

The first part of this thesis starts from the polynomial spline function space, and introduce the B spline function. Then, we find a group of base functions consisting of B spline functions with the properties of local support and symmetry. Finally, the cubic spline interpolation function is represented by B spline function, and the coefficient matrix is written.

In the rest of this thesis, we expatiate the application of spline function from three aspects. Firstly, we use the B spline function to evaluate numerical differentiation and numerical integration, which is compared with the traditional numerical method. Secondly, we solve the initial value problem of ordinary differential equation according to the B spline function, and derive an implicit formula. The implicit formula is stable and the local truncation error is O(h⁵), and the global truncation error is O(h⁴). Because the implicit format is not convenient for calculation, we use Euler’s prediction - correction method to improve this format, and get a format for easy calculation, and its local truncation error is at least O (h⁴). And we compare it with Euler’s prediction-correction method and fourth order Runge-Kutta method. The result is satisfactory. And then we make the least squares fitting by B spline function and compare it with polynomial least squares fitting. The result shows that using B spline function as the base function is better. Finally, we analyze the influence of the times and the number of nodes of B spline function on fitting results. The results show that, as the number of nodes is more, the fitting effect is better, but the mean square error decreases gradually. When the number of nodes are fixed, with the times increase, the calculation quantity increases continuously, and the mean square error is increasing gradually. But they are all on the same order of magnitude and can meet the required precision. Therefore, combined with the analysis of the two, we can choose the appropriate times and number of nodes to achieve a better fitting result quickly.

Keywords: B spline function; Numerical differentiation; Numerical integration; Ordinary differential equation; Least squares method.

目 录

第1章 绪论 1

1.1 选题背景和意义 1

1.2 国内外研究现状 2

1.3 本文的主要工作 3

第2章 多项式样条函数空间与三次样条插值函数 4

2.1 多项式样条函数空间 4

2.2 三次样条插值函数及其边界条件 5

2.3 三次样条插值函数的建立 6

2.4 三次样条插值函数的性质 8

2.5 三次样条插值函数的误差估计与收敛性 9

第3章 B样条函数 10

3.1差商定义及其性质 10

3.2 B样条函数的定义 11

3.3 B样条函数的性质 13

3.4扩充分割 15

3.5 B样条函数的计算 16

3.6 三次样条插值函数的B样条函数表示 17

3.6.1 第一类、第二类插值问题下的B样条函数表示 18

3.6.2 第三类插值问题下的B样条函数表示 19

3.6.3 计算实例 20

第4章 B样条函数的应用 22

4.1 数值微商和数值积分 22

4.1.1 数值微商方法 22

4.1.2 数值微商计算实例 23

4.1.3 数值积分方法 24

4.1.4 数值积分计算实例 26

4.2 常微分方程初值问题 27

4.2.1 常微分方程初值问题数值方法推导 27

4.2.2 常微分方程初值问题计算实例 29

4.3 最小二乘法 30

4.3.1 最小二乘法原理 30

4.3.2 多项式最小二乘法 32

4.3.3 样条最小二乘法 32

4.3.4 次数和节点个数对拟合结果的影响 34

第5章 总结与展望 35

参考文献 36

附录 38

致谢 40

第1章 绪论

1.1 选题背景和意义

1946年，Schoenberg^[1]提出了样条函数这一概念，从此，样条函数正式进入众多研究学者的眼中。到20世纪70年代左右，人们对航空、造船、机械设计和制造等行业应用计算机辅助设计的需要不断增加，产生了一系列有关几何外形数学模型与数据平滑等方面的问题，样条函数为这些问题提供了一个简单而有效的方法。

样条函数是由若干个分段多项式定义的特殊函数^[2]。它的每个相邻分段上的多项式之间具有某种连续性质，由此使得它保持了多项式与有理式的简单性和可逼近性，它还在各个分段单元上保持了相对独立的局部性质^[3]。除此之外，它还具有数值稳定性、收敛性、递归性、凸性、局部支撑性等诸多良好性质。

正是因为样条函数具有上述所列举的许多良好的性质，所以它被广泛应用于各个方面。例如：当函数不便求导时，可以利用低次样条函数插值求函数的数值微商；当函数求积较为困难时，可以建立样条插值函数来求解其数值积分；当微分方程精确解难以计算时，可以利用样条函数求解方程的数值解；当利用多项式基函数进行最小二乘法来拟合数据所得到的效果并不是很好时，可以使用样条基函数进行数据拟合来得到更好、更稳定的拟合结果等等。不仅如此，样条函数在计算机辅助设计中也有很大的作用，它在曲线、曲面信息的表示、逼近、拟合和分析等方面取得了重要的成果；一些常见的大型几何设计软件都是使用样条函数作为主要工具。

B样条函数是一种特殊的、非常重要的样条函数，它被广泛应用到各个领域中，其理论工作在1947年由Curry和Schoenberg^[4]给出，由于B样条函数构造性的结果使其在样条理论中举足轻重。起初B样条函数是利用高阶差商来定义的，这种定义方式有可能会产生数值不稳定性。随后，De Boor利用B样条函数的递推关系^[5]定义B样条函数，这种定义方式不同于高阶差商，但却是由高阶差商定义所推导出来的。B样条函数有很多种类，常见的类型有等距节点B样条函数、非等距节点B样条函数、周期B样条函数等。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：