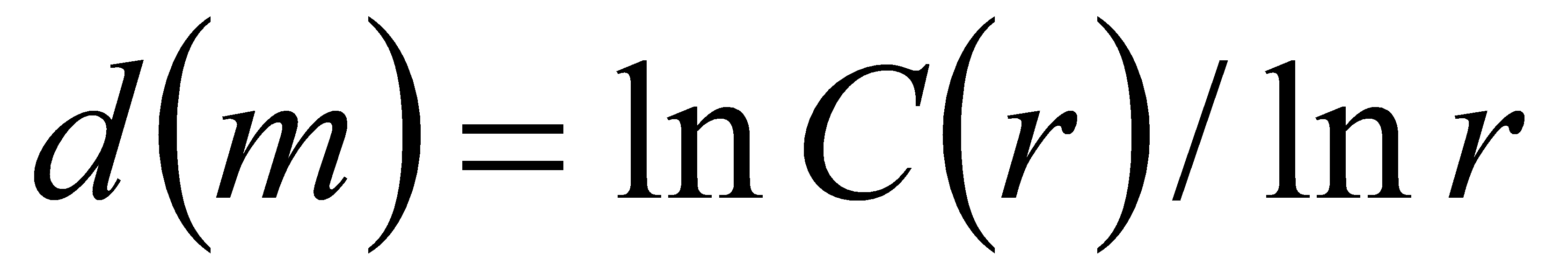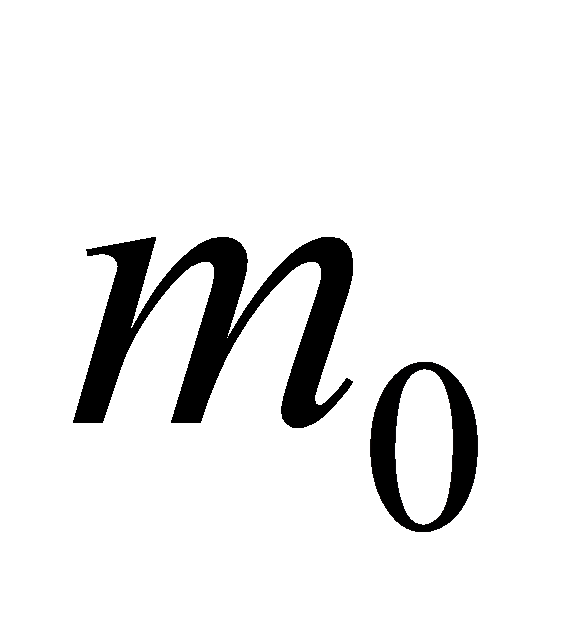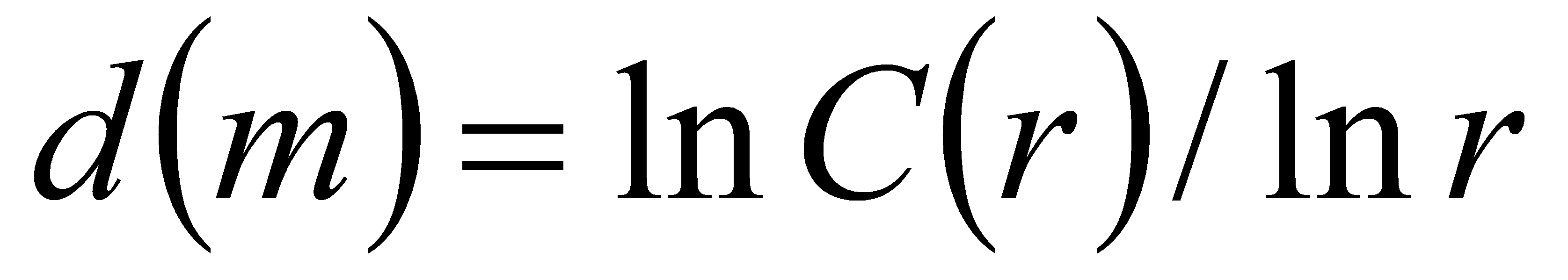分形理论及其对中证500股指期货的研究毕业论文
2020-07-07 21:54:02
摘 要
一直以来,欧几里德几何学研究的都是规则的形体,而大自然中大多数的物体都是不规则的。因此一个新的概念——“分形”被提了出来,它可以依据公式来构造自然界中的一些不规则的物体,并分析其特性。作为一门新兴的学科,分形发展的时间虽然很短,至今也不过40多年,但它在数学、物理、化学等多个领域都有着广泛的应用。分形维数是分形几何的中心概念,是用来判断是否为分形的一个参量。如今,许多经济学家也开始用分形理论研究一些经济现象,例如股票价格的变化。本篇论文将借助分形理论的数学知识,用C-C法计算中证500股指期货的时间窗口和时间延迟,再利用G-P算法计算中证500股指的关联维数,对其进行实证分析,若所得到的维数不是整数,则其具有分形特征。
【关键词】:分形 分形理论 分形维数 关联维数
Research on Fractal Theory and Stock Index Futures of China Stock Market 500
Abstract
Euclidean geometry has always studied regular bodies, while most objects in nature are irregular. Therefore, a new concept, "fractal", has been proposed, which can be used to construct some irregular objects in nature and analyze their properties. As a new subject, fractal has been widely used in many fields, such as mathematics, physics, chemistry and so on. Fractal dimension is the central concept of fractal geometry and a parameter used to judge whether it is fractal or not. Today, many economists also use fractal theory to study some economic phenomena, such as stock price changes. In this paper, with the help of the mathematical knowledge of fractal theory, the time window and time delay of CS500 stock index futures are calculated by c-c method, and then the correlation dimension of CS500 stock index is calculated by g-p algorithm, and the empirical analysis is carried out. If the dimension obtained is not an integer, it has fractal characteristics.
Key Words:Fractal;Fractal theory; fractal dimension; correlation dimension
目录
摘 要 Ⅰ
Abstract 3
第一章 绪论 1
1.1来源和背景 1
1.1.1分形的来源 1
1.1.2中国股指期货的发展历程 2
1.2国内外现状对比分析 3
1.3研究的方法和内容 4
第二章 分形的数学理论知识 5
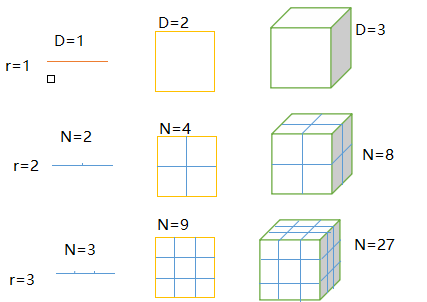
第三章 分形维数的定义及计算 8
3.1豪斯多夫维数 9
3.2 盒维数 10
3.3关联维数 11
3.4 相似性维数 12
3.5 容量维数 13
3.6 信息维数 14
第四章 以中证500股指期货为例进行实证分析 15
4.1中证500股指期货的介绍 15
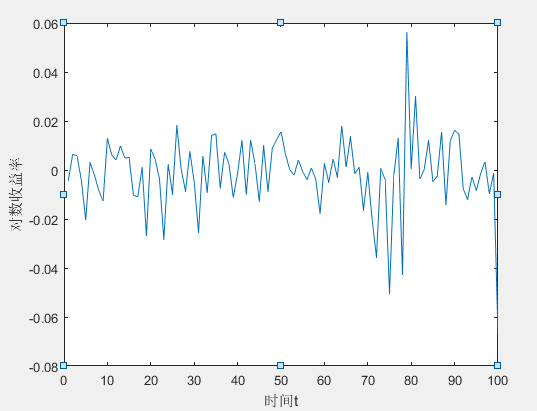
4.2实证分析 15
第五章 总结与展望 20
第一章 绪论
1.1来源和背景
1.1.1分形的来源
布列塔尼的海岸线究竟有多长?这是一个困扰了人们很多年的问题。Mandelbrot针对这一问题展开了研究,并提出了分形(Fractal)的概念:分形是从“不规则的或断裂的”拉丁形容词“fractus”中派生出来的。Mandelbrot认为海岸线就是一个天然的分形。他发现无论将海岸线怎样放大,看到的部分都是相似的,于是Mandelbrot便提出了海岸线具有自相似性的特征,并把这些整体与部分存在一定相似的形体称为分形(fractal)。1973年Mandelbrot在给法兰西学院的学生授课的时候,分形几何的构想在他的脑中迸发。分形的概念最早由Mandelbrot于1975年时提出,“分形”这个词的由来也很有意思,这是Mandelbrot从他儿子的拉丁文字典中翻出来的,愿意是fractus(拉丁文的形容词)。Mandelbrot于1977年出版了《分形:形态,偶然性和维数》,这是他出版的第一本书,后来这本书为分形理论发展做出了不可磨灭贡献,成为物理学史上一个重要的里程碑,这意味着分形理论正式诞生了。随后,Mandelbrot出版了《自然界的分形几何》,这本书的发布成为了后来分形理论的理论基础,并在此基础上,分形几何也随着分形理论的发展而逐渐形成。其实,除了布列塔尼的海岸线之外大自然中还存在着许多其它的分形,例如连绵不绝的山川、天空中飘浮的云朵、冬天的雪花、树叶的纹理等都具有自相似性的特征,所以分形理论也可以被称为是一门大自然的几何学。周海中教授(中国的著名学者)曾经这样评价分形几何:分形几何不仅完美的展现出数学的美,同样也揭露了世界的本质,并且改变了人们对自然奥秘的理解方式;可以说分形几何可以真正的去描述大自然,而且对它的研究也可以拓展了人们的认知范围。但是Mandelbrot在他的作品中强调了自然界中的分形与数学中的“分形集”是有很大区别的,只是这个区别并不太明显。英国数学家Kenneth.Falconer也在他的著作《分形几何 数学基础及应用》中说道:在现实生活中,自然界中并没有严格意义上的分形,同样也没有严格意义上的圆和直线。
分形理论是一门新的学科,它出现将整体与部分,混乱与规则,有限与无限,连续与间断联系到了一起,在这些看似没有关系的东西中,找到了它们之间存在的相似性。从分形理论的出现到现在也不过40多年,很多理论还有待进一步的研究,但当今社会对分形理论的应用发展已远远超过其理论的发展。目前,对分形理论的应用已涉及了数学,物理,地理,经济等多个领域。如在地理上借助分形理论优化城市的布局,使城市的地理环境得到更合理的利用[25];利用分形几何学原理模拟自然景象[30];运用分形理论对股票价格进行分析[31]等。越来越多的学者加入到分形的研究与讨论中,如各个领域涉及分形的学术论文和书籍在不断增加,国际上也不断开展了有关分形的各种研讨会。由此可见,分形在未来的应用会越来越广泛,而我们今后的生活可能也会与分形息息相关。甚至约翰·惠勒(美国物学大家)曾经说过:如果今后有谁不熟悉分形,他就不能被称是一个研究科学的人。
1.1.2中国股指期货的发展历程
股票价格指数期货又被称作股指期货。美国的堪萨斯城期货所交易所在1982年向外推出了有史以来第一个价值线综合指数期货合约,这是历史上第一个股指期货品种,从此以后,越来越多的股指期货在股票市场上出现,并蓬勃发展。股指期货就是用一些股票价格指数作为标准的物品,交易地点固定在交易所,然后交易的双方一起签署标准化的合约。这样做的目的是在未来的某一个时间以预先定好的价格指数大小进行交易,并在到期后以现金的方式结算差额。但股指期货在我国的推出却是历经了坎坷,海南证券交易所曾尝试推出深圳股指期货,可最终因为股价指数的编制不合理,以及当时我国的利率、汇率还未放开而失败。沪深300指数期货于2010年4月16日在中国的金融期货交易所挂牌上市,这标志着我国的股指期货市场迈入新发展的阶段。
股指期货作为一种金融衍生工具,具有金融衍生品的特性,即套期保值、杠杆性等。股指期货的交易在原则上与其他证券的交易是相类似的,但是股票价格指数却是经过了统计处理,并且是提前确定好的。合约价值就是指股指期货合约的股票价格指数和合约乘数的乘积,但是股票价格指数的目的是作为一种指标,即反映金融服务机构编制或者股票市场的价格波动水平。所以,股票市场和股指期货市场紧密相连。中国的股指期货市场起步较晚,但沪深300股指期货作为股指期货的代表,目前已有了许多对沪深300股指期货的研究,许多学者通过计算其分形维数,分形维数越大,股票价格的波动越大,股票市场越活跃,以此来确定其分性特征,从而确定了中国的股票市场是分形的。那么中证500股指期货作为股指期货的一种,是否也满足这样的特征呢,本文将运用分形理论知识针对中证500股指期货展开研究。
1.2国内外现状对比分析
H.E.Hurst(英国水文专家)通过分析尼罗河水库的库容量与水流量之间的关系,得到了一种分析方法来描述水库的长期蓄水能力,即根据偏的分形布朗运动的重标极差(R/S)来分析。然后他在1972年第一次将重标极差分析美国的股市,并检验美国股市是否具有分形的特点。后来A. M. A. El-Sayed等人[1]研究了复变量logistic方程连续动力系统的动力学性质、平衡点、局部和全局稳定性、混沌和分岔。证明了齐次Lyapunov指数存在唯一稳定解。Wang Rui等人[2]通过计算金融时间序列的最大Lyapunov指数,构造了修正结构多重变化模型检验金融结构变化,并对2005年至2012年金融危机期间标准普尔500指数日数据进行实证分析。M. Trojanowska[3]利用自相似分形模,logistic模型以及启发式较差模型对电能销售进行预测,并对模型进行评价
Wolf A和他的工作团队[4]发表了在时间序列里预测Lyapunov指数的论文,还说明了混沌是可以分区的,但吸引子的维数不能太高。Diogo Baptista和Ricardo Severino[5]介绍了计算最大Lyapunov指数的方法,并运用此方法研究了前、后轨道保持有界的点集最大Lyapunov指数的行为,以及最大Lyapunov指数可以假设的最大值。
我国虽然在这一领域中的起步较晚,但近年来在这一领域的研究也取得了巨大的进步,尤其是在我国的股票市场和期货市场中,他们也进行了诸多研究。
陈昭和王国臣[6]利用Hurst指数指数分析理论方法和BDS测试对1997年1
月2日-2001年12月31日共5年间深圳成份指数进行了实证分析。结果表明我国深圳股票市场的波动具有明显的混沌特征。姜灵敏[7]更是通过几个案例表明我国股票市场是一非线性系统。李志勇[8]等人根据去除小极值保留真正极值得到理论构造生成元,再根据上证中和综合指数(分形迭代函数系统生成)得到了趋势模拟图表。此外,他们还利用尺度C定义了一种新的维数栏维 ,并分别计算上证指数的栏维和关联维数,表明股票市场存在混沌分形特征。谭洁[9]通过考察上证综合指数和深圳成份指数的对数收益序列,分别计算两个市场的时间尺度分形维和概率空间分形维,发现这两个市场均存在显著的分形特征,股票市场的价格波动不是随机变化的,而是以一定的概率呈列维稳定分布的,从而证明分形市场假说。齐佳[10]通过R/S分析法与V/S分析法计算我国股指期货市场的主力合约和加权合约的hurst指数,发现我国的股指期货市场具有明显的分形特征。
,并分别计算上证指数的栏维和关联维数,表明股票市场存在混沌分形特征。谭洁[9]通过考察上证综合指数和深圳成份指数的对数收益序列,分别计算两个市场的时间尺度分形维和概率空间分形维,发现这两个市场均存在显著的分形特征,股票市场的价格波动不是随机变化的,而是以一定的概率呈列维稳定分布的,从而证明分形市场假说。齐佳[10]通过R/S分析法与V/S分析法计算我国股指期货市场的主力合约和加权合约的hurst指数,发现我国的股指期货市场具有明显的分形特征。
1.3研究的方法和内容
本文由五个部分构成,首先是文章绪论,讲述了关于分形的产生及发展,中国股指期货的发展现状,以及国内外已有的对分形理论的研究。第二部分是关于分形的数学理论知识,还有分形理论在数学研究中的具体应用。论文的第三部分研究了分形维数不同的定义,以及在不同定义下分形维数的计算方法。第四部分先是利用了C-C法计算中证500股指期货的延迟时间和时间窗口,然后在通过G-P算法计算中证500股指期货的关联维数,对其进行实证分析。论文的最后一部分则是对分形理论的总结,对其在股票市场上未来应用发展的展望。
分形的数学理论知识
数学中的分形可以说是从康托尔集(Cantor Set)[11]开始萌芽的。康托尔集是一种人们最了解的,也是一种最容易构造的分形,它在1883年由德国数学家格奥尔格·康托尔。取闭区间[0,1],去掉该区间中间的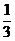 即
即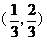 ,剩下
,剩下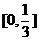 和
和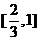 两个闭区间,将剩下的两个区间分别进行相同的操作,即去掉
两个闭区间,将剩下的两个区间分别进行相同的操作,即去掉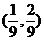 和
和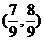 ,剩下
,剩下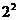 长度为
长度为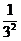 的闭区间
的闭区间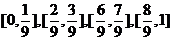 ,在进行了
,在进行了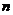 次操作之后,剩下的
次操作之后,剩下的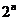 个长度为
个长度为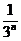 的闭区间
的闭区间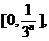
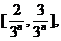 …,
…,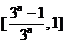 ,当
,当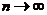 时,每个小区间的长度趋向于0,由闭区间套定理,用数轴来表示即是一个点。区间[0,1]上没有被去掉的博雷尔集被称作康托尔集。
时,每个小区间的长度趋向于0,由闭区间套定理,用数轴来表示即是一个点。区间[0,1]上没有被去掉的博雷尔集被称作康托尔集。

图2-1 康托尔集

相关图片展示: