摘 要

不等式是中学数学教学中的一个关键点和困难点，中学生在学习不等式和应用不等式中有很多困难，柯西不等式是常见的不等式，也是一个非常关键的不等式，它具有简洁，对称的美感和广泛的应用引起了诸多学者的讨论.柯西不等式与中学数学密切相关，它经常出现在中学代数问题、几何问题中，在竞赛型题目中也诸多涉及，能够了解柯西不等式的本质，掌握其结构特征，便能灵活应用，可以使一些问题很容易得到解决.不仅是柯西不等式的一般形式，而且它的其他形式和一些变式也在本文中被研究，有助于学生透彻了解柯西不等式的本质；接着以例题的形式讨论柯西不等式在中等数学中的应用，有助于学生更具体地感受到柯西不等式的结构特征，加强理解提高解决问题的能力；最后转化角度总结出柯西不等式在初高中数学的教学现状，针对教师探讨了进一步的教学.

关键词：柯西不等式 方程 代数 三角 向量

The Application of Cauchy Inequality in Elementary Mathematics

Abstract

Inequality is a key and difficult point in middle school mathematics teaching. Middle school students have many difficulties in learning inequalities and application inequalities. The Cauchy inequality is not only a common inequality, but also a very significant inequality. It has a concise, harmonious, symmetrical aesthetic. And extensive application has caused many scholars to discuss. Cauchy inequality and high school mathematics are closely related, it often appears in the middle school algebra problems, geometry problems, in also many involved in the title race type, able to understand the nature of Cauchy inequality, mastering its structural characteristics can be flexibly applied and can make some problems easily solved. Not only is the general form of Cauchy inequality, but also its other forms and some variants are studied in this article, which helps students thoroughly understand the nature of Cauchy inequality; Then in the form of examples to discuss the application of Cauchy inequality in secondary mathematics, help students to feel a more detailed structure features of Cauchy inequality, strengthen the understanding to improve the ability to solve the problem; Finally, the teaching status of Cauchy inequality in middle and high school mathematics is summarized, and further teaching is discussed for teachers.

Key words: Cauchy inequality; Equation; Algebraic; Triangle; Vector

目录

摘要 I

Abstract II

第一章 引言 1

1.1 研究目的和意义 1

1.2 相关研究背景 1

第二章 柯西不等式的相关理论及证明 2

2.1 柯西不等式的一般形式 2

2.2 柯西不等式一般形式的证明 2

2.2.1 构造函数法 2

2.2.2 比较法 2

2.2.3 向量内积法 3

2.2.4 数学归纳法 3

2.3 柯西不等式的向量形式 4

2.4 柯西不等式的向量形式的证明 4

2.5 柯西不等式的三角形式 4

2.6 柯西不等式的三角形式的证明 4

2.7 柯西不等式的几个变式 5

第三章 柯西不等式在初等数学中的应用 7

3.1 柯西不等式在中学代数中的应用 7

3.1.1最值问题 7

3.1.2 不等式问题 7

3.1.3 求值问题 8

3.1.4 求参数范围 9

3.2柯西不等式在中学三角问题中的应用 10

3.2.1 最值问题 10

3.2.2 不等式问题 11

3.2.3 求值问题 12

3.2.4 等式的证明问题 12

3.3 柯西不等式在中学几何中的应用 13

3.3.1 在平面几何中的应用 13

3.3.2 在立体几何中的应用 13

3.3.3 在解析几何中的应用 14

第四章 研究结论和建议 16

第五章 结语 17

参考文献 18

第一章 引言

1.1 研究目的和意义

在我们初高中的数学学习中，学习了很多不等式的相关知识，有解不等式，有证明不等式等等，其中，柯西不等式在学习过程中起到了十分重要的作用.本文旨在对柯西不等式的基本知识和方法进行一些梳理，并探讨了其在典型题目中的应用，希望能对柯西不等式在初等数学中的应用做一些有益的研究和为初高中学生对于柯西不等式的学习做一些有益的指导和示范，以此提高广大初高中学生解决和证明不等式问题的能力、运算能力、逻辑推理能力.

1.2 相关研究背景

时代不断发展，历代学者对柯西不等式进行了更深层次的研讨与学习，他们针对不同的领域都进行了深入的学习，到目前为止已经有了很多严谨成熟的理论成果，其中对中学数学领域的研究也必不可少，他们有的在代数和三角问题的解决等方面进行探索总结；有的则是探讨了柯西不等式解题的变形技巧；有的研究了柯西不等式的各种形式在中学几何中的应用；有的全面严谨地探讨了柯西不等式的多种证明方法；也有学者讨论了柯西不等式在高中证明中的巧用，为学生解题带来方便；通过实例研究柯西不等式简单的变式应用，介绍柯西不等式的常见应用范围和方法并且以此来解决竞赛问题；也有学者站在教师的角度，在如何教好柯西不等式这一课进行了研究并且给出珍贵的建议；通过转化角度总结出柯西不等式在初高中数学的教学现状，针对教师探讨了进一步的教学；其中不仅是中国的学者，更有外国学者对柯西不等式也是有着浓厚的兴趣，他们总结了柯西不等式的应用和解决过程.正是这些古今中外的学者丰富了柯西不等式的研究史，方便了我们对柯西不等式的理解和运用.

第二章 柯西不等式的相关理论及证明

2.1 柯西不等式的一般形式：

设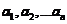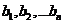，都是实数，那么有