杭 州 师 范 大 学

本科生毕业设计（论文）外文文献翻译

圆锥曲线旋转变换教学中的问题和解决建议

原文作者 Tuba ADA, University of Anadolu, Eskişehir (Turkey).

Aytaccedil; KURTULUŞ, University of Eskişehir Osmangazi, Eskişehir (Turkey).

专业：数学与应用数学（师范） 学生姓名：林佳佳

指导老师姓名：叶立军

摘要：圆锥曲线，是由一平面以不同角度截二次锥面得到的曲线，包括圆、椭圆、抛物线、双曲线。这些曲线可以根据不同的角度在不同的位置找到。于是可以将旋转变换应用于曲线，以便将其主轴置于水平位置。本研究的目的是找出数学准教师在有关圆锥曲线的旋转变换上所遇到的问题，并为这些问题制定解决方案。40名准教师参与了此项研究。研究人员设计并实施了一项行动计划，以便从准教师所遇到的问题出发，解决这些问题。在研究结束时，可以确定的是准教师们绘制曲线图的成功程度有所提高。

关键词：圆锥曲线；坐标变换；旋转变换；行为研究

引言

圆、椭圆、抛物线、双曲线被定义为圆锥曲线，是由一平面以不同角度截二次锥面得到的曲线，如下图1.

图1. 一平面截二次锥面得到的曲线

圆是通过由平行于圆锥底面的平面去截此圆锥所得，椭圆是一平面在具体角度下所截此圆锥所得，抛物线是通过取与锥侧平行的平面截面得到的，双曲线是通过平行于圆锥轴线的平面相交得到的。当分析这些曲线时，可以发现它们在不同的位置(主轴是水平的、垂直的或任何倾斜的线)。根据这些曲线的位置可以得到代数方程。

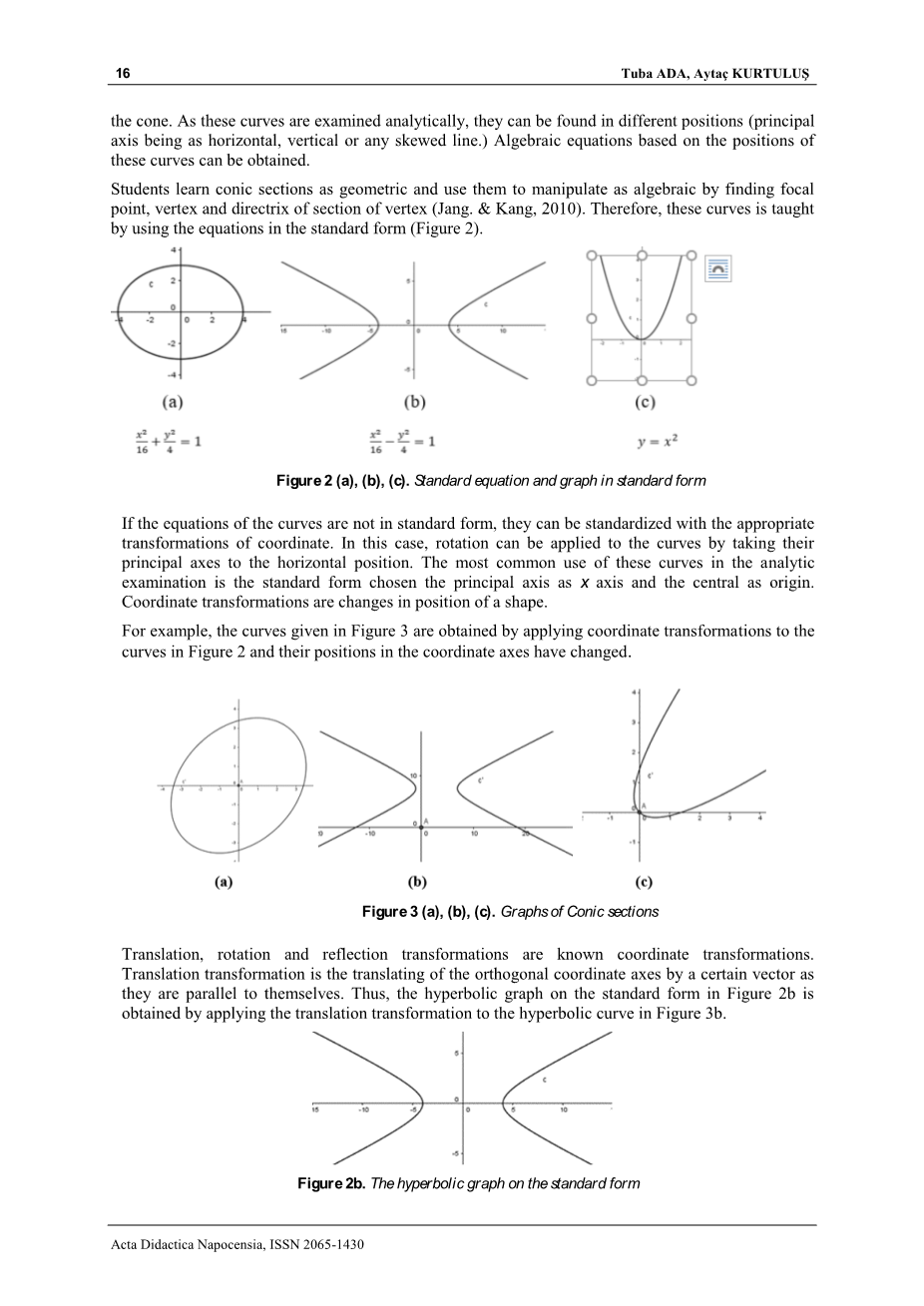
学生以几何的方式学习圆锥曲线，并通过寻找焦点、顶点和准线来进行代数运算。因此，这些曲线是用标准形式的方程来教的（图2）。

图2(a),(b),(c). 标准形式的标准方程及图象

如果曲线方程不是标准形式，可以通过适当的坐标变换进行标准化。在这种情况下，可以通过将它们的主轴移到水平位置来对曲线进行旋转。这些曲线在分析检验中最常用的形式是选择主轴为x轴、中心为原点的标准形式。坐标变换是形状位置的变化。

例如，图3中给出的曲线是通过对图2中的曲线进行坐标变换得到的，并且它们在坐标轴上的位置发生了变化。

图3(a),(b),(c). 圆锥曲线的图象

平移、旋转和反射变换是已知的坐标变换。平移变换是指当正交坐标轴与它们自身平行时，将它们平移成一定的向量。因此，通过对图3b中的双曲线进行平移变换，得到图2b中标准形式的双曲线。

图2b. 标准形式的双曲线

图3b. 将平移变换应用于双曲线

将方程(曲线)给出的点集合转换为给定的向量，得到新的图象(图3b)。因此，通过平移变换可以得到标准形式的曲线方程。学习者能够画出曲线上的点集所代表的图形。然而，在给定的代数方程中，平移关系并不总是足以求出一组点的几何轨迹。在这种情况下，还需要其他坐标转换。

旋转变换是这些坐标变换中的一种。旋转变换定义为x轴和y轴围绕一个初始点旋转一个特定角度。这样，通过旋转变换，曲线的位置在平面上的某一点周围发生一定角度的变化。例如，在图4中，将第一个形状围绕原点顺时针旋转45度，以获得标准形式的第二幅图象。

在图4中，沿原点顺时针旋转45度，得到代数方程所给出的椭圆标准方程。

图4. 第二个椭圆为第一个椭圆绕原点旋转了45度后的新形状

Ada and Kurtulus (2010, p.91)认为，对复杂的代数方程进行适当的坐标变换，化简为标准形式，就可以确定曲线表示的是哪条曲线。另一方面，通过确定对一组几何定义的点进行旋转变换的旋转点、角度和方向，可以确定曲线的新位置。在这种情况下，根据Hollebrand（2003)，坐标变换是重要的，因为它为学生提供了考虑重要数学概念(如函数、对称性）的机会，提供了一个可以将数学看作是一门相互依存的学科的背景，并为学生提供了发展高水平推理技能的机会。

根据NCTM（2000），坐标变换是一个帮助学生发展空间推理和可视化技能的概念。课程支持对各个层次的学生进行轮岗教学(NCTM, 2000;. McNiff, J., Lomax, P., amp; Whitehead, J., 1996). 此外，根据对文献的研究，似乎所有年龄段的学生都很难处理与旋转相关的概念(Yanik amp; Flores, 2009)。

Ada和Kurtulus(2010)的研究表明，在确定给定曲线的类型时，应用适当的平移或旋转变换有助于确定曲线的类型。人们认为，将坐标变换后的复杂曲线方程简化为标准形式，有利于以代数的方式确定曲线的类型。然而，当学生用旋转变换或解释问题时，研究者在教学经验上遇到了困难。

本研究的目的是寻找解决圆锥曲线旋转教学中遇到的问题以及如何解决这些问题的方法。

2. 方法论

2.1 研究模型

研究人员确定了数学准教师在处理坐标变换时遇到的问题，并指出了他们在将方程旋转和绘制新方程图形时遇到的困难。在本研究中，用准备好的活动来解决这些问题，并作为一项行动研究加以应用。行动研究具有周期性特征，可以确定和识别问题，并确保收集信息、扫描资源、制定和改进解决问题的行动(Johnson,2002; McNiff, Lomax, amp;Whitehead, 1996).

2.2 参与者

共有40名在某州立大学学习2016-2017学年秋季学期《解析几何1》课程的小学三年级数学准教师参加了本研究。备课计划用了三个星期。

2.3 数据收集

数据收集从准教师们对案例确定过程中开放式问题的解决方案和实施过程中评估问题的解决方案。此外，研究人员在整个研究过程中都进行了课堂观察。

2.4 数据分析

本研究采用结构化问题和观察技术获取数据。通过分组对信息进行解释，同时对来自观察和开放式查询的数据进行分析。对从结构化查询中获得的数据进行描述性分析。在描述性分析中，为了清晰地反映学生的思维方式，从学生的论文中引用和例子，数据以原始的形式转移。

2.5 研究过程

研究过程分为三个阶段。第一阶段，从理论上解释了准教师对坐标变换中的旋转变换的概念理解。在这门课的教学中，代数和几何方法都被强调。用代数方法给出了曲线的旋转变换关系和方程的变化。旋转变换关系定义如下(*)式。

几何上考虑了两种方法(Kaya, 2012)。第一种方法是绕着原点旋转坐标轴。在本例中，旋转下的图象与给定的点集是相同的(如图5)。

图5 坐标轴以一定的角度围绕原点旋转

第二种方法是围绕原点旋转这些点。在这种情况下，点集和图象是不一样的(如图6)。

图6 椭圆绕原点旋转一定角度

在第一种方法中，只旋转坐标轴，曲线的位置不改变。在本研究中，考虑第二种方法，因为圆锥曲线的目的是观察坐标的转换和位置的变化。

第二阶段是确定情况。在这一阶段，我们采用了开放式的问题测试，以确定探索这些旋转变换方法的准教师们对这一主题的理解程度。在圆锥曲线方程解的代数运算过程中，一些准教师错误地绘制了曲线的图象。

Geogebra软件是一种动态几何软件，它除了代数运算外，还用于求解在应用阶段确定其类型所需的曲线方程，这是第三阶段的应用，以解决这些准教师在几何上经历的问题。研究人员向准教师们提出了不限成员名额的问题，以观察这些应用是否充分。

3. 调查结果

在本研究中，遵循前几章的研究过程，按照平面上坐标变换的错误修正进行上课。对参与者进行编码。以下按顺序列出行动计划的案例和应用阶段的确定结果。

案例确定与反馈(第二阶段):在这个阶段，要求考生教师定义在开放式问题测试中给出代数方程的曲线的类型和图形。为准教师提供了一小段时间来解决这个问题。在第一个问题的这段时间里，一些准教师试着把给定的等式四舍五入到一个正方形，而一些没有做任何事情。在图7中可以看到，S11编码的准教师试图将等式四舍六入来完成正方形，但无法得出标准形式。

图7 编码为S11的准教师的解法

准教师将曲线方程插入到几何学中，得到图形。因此确定了类型。“需要做些什么才能把这个等式变成标准形式?”回答为变换应用。对于这个方程，准教师支持坐标变换的解。在此基础上，有的应用了平行变换和垂直平移变换，有的应用了旋转变换。应用平移变换的S30编码的准教师的解如图8所示。在检验解时，应用了平行垂直平移变换公式()。因此，通过求出a和b的值，准教师们试图消去x和y项。然而，由于变换不正确，方程没有得到标准形式。

在这种情况下，研究人员解释说，变换应该根据曲线方程的项来选择，为了去掉“xy”等项，旋转变换更合适。因此，那些有错误解的人通过旋转进行变换，使方程变成标准形式。图9显示了S11编码的准教师的正确解法。

图8 编码为S30的准教师的解法

图9 编码为S11的准教师的正确解法

有些准教师即使在方程上应用了合适的变换，但由于计算错误，仍然无法得出标准形式。图10显示了S22编码的准教师的解决方案，他通过旋转变换，但得到了错误的方程，因此由于计算错误绘制了错误的图形。

图10 编码为S22的准教师的解法

当要求在同一坐标系中绘制同一曲线的图象和主体时，一些准教师不能将曲线的标准图插入到正确的坐标系位置。另一方面，一些准教师则采用了第一种旋转变换的方法，即在曲线的位置不变的情况下，对坐标轴进行旋转。然而，在本研究中，评估是基于第二种旋转方法的。例如，如图11所示，S14编码的准教师确定了错误的曲线图，因为焦点必须在坐标轴上。图12显示了S15编码的准教师的解法，它使用第一种旋转变换的方法。

图11 编码为S14的准教师的解法 图12 编码为S15的准教师的解法

应用程序(第三阶段)：在这个步骤中，首先为了那些无法画出图的准教师们，前一步中正确地注意到正确的图纸，使用Geogebra动态几何软件，曲线的形象图时旋转围绕其起点与45度的角度。之后，又对准教师进行了与第一个类似的开放式问题测试。

大多数准教师通过将旋转的适当变换应用于曲线，成功地将方程转化为标准形式。然而，当涉及到图形的绘制时，又遇到了一次麻烦。为了克服这些问题，研究的每个参与者都在Geogebra软件中输入曲线方程，并观察曲线图和曲线图象的角度。 图13、14和15给出了Geogebra软件应用步骤中准教师的图纸。

图13 椭圆的图象以及标准形式的图象

图14 双曲线的图象以及标准形式的图象

图15 抛物线的图象以及标准形式的图象

最后对准教师进行开放式问题测试，以了解解决方法对克服案例步骤确定所面临的困难有多大的帮助。对所获资料进行描述性分析。主题是基于准教师的解决方案创建的。主题呈现见下表1。

表1 40名准教师根据问题的答案分布表