探讨函数最值问题外文翻译资料
2023-01-12 11:28:13
探讨函数最值问题
Kiryl Tsishchanka New York University
摘要:本文是第四章的第一节,主要内容是介绍函数的最大值和最小值的概念以及会求解一般函数的最值问题.本文用到的主要方法是数形结合,通过大量的练习让学生熟练掌握求解一般函数最值问题的解题方法.
关键词:函数;最值;
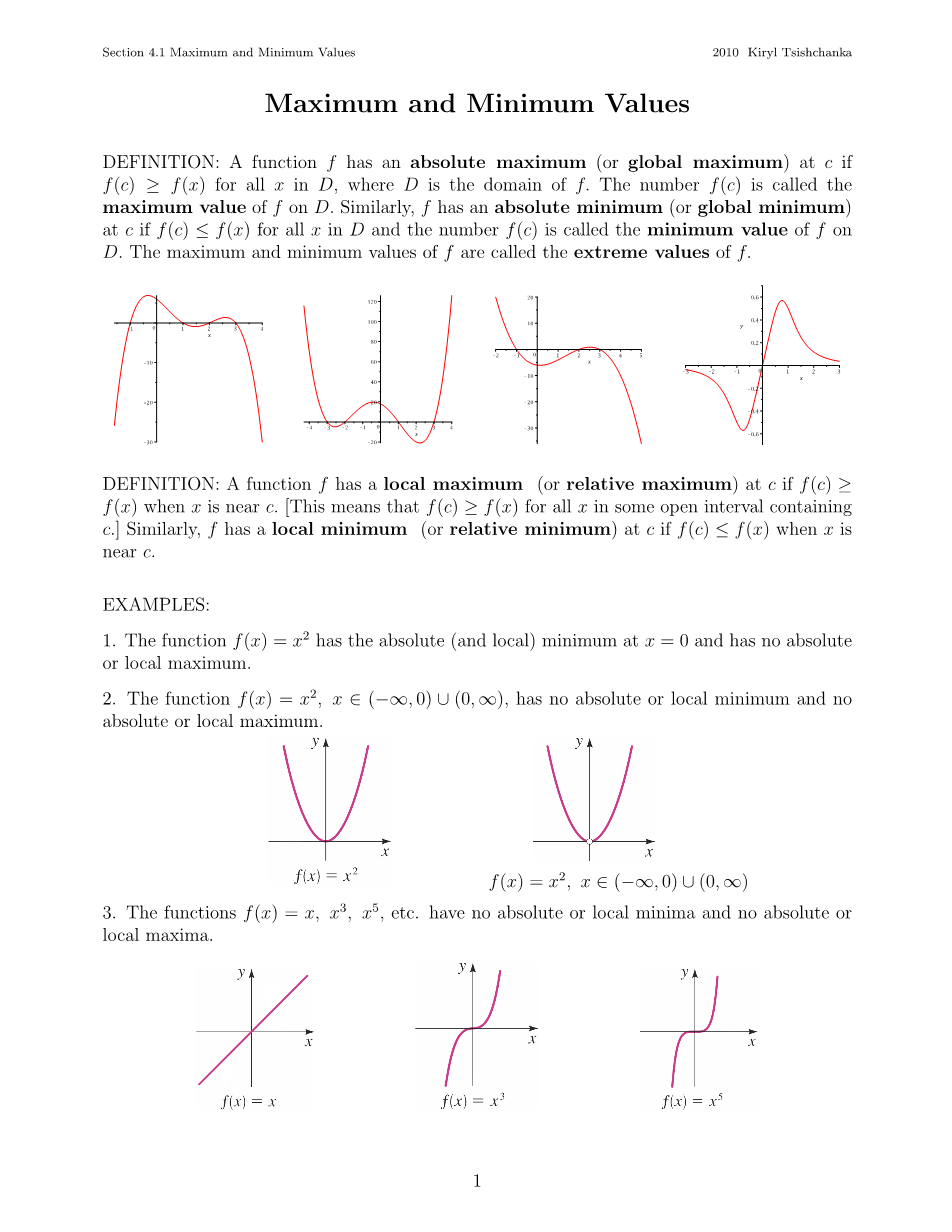
定义:如果一个函数在上有一个绝对最大值(或是全局最大值),对所有的定义域上的,它满足,这个值就被叫做这个函数在上的最大值.同理可知,如果一个函数在上有一个绝对最小值(或是全局最小值),对所有的定义域上的,它满足,这个值就被叫做这个函数在上的最小值.函数上的最小值和最大值统称为函数的最值.
定义:如果一个函数存在一个,当自变量接近于时,它满足,这个值就被叫做这个函数上的相对最大值(或是局部最大值),也就是说对所有在开区间里的,都有.同理可知,如果一个函数存在一个,当自变量接近于时,它满足,这个值就被叫做这个函数上的相对最小值(或是局部最小值).
例如:
- 函数在时取到最小值且没有最大值.
- 函数当时,既无最大值也无最小值.
- 函数,等等,都没有最大值和最小值.
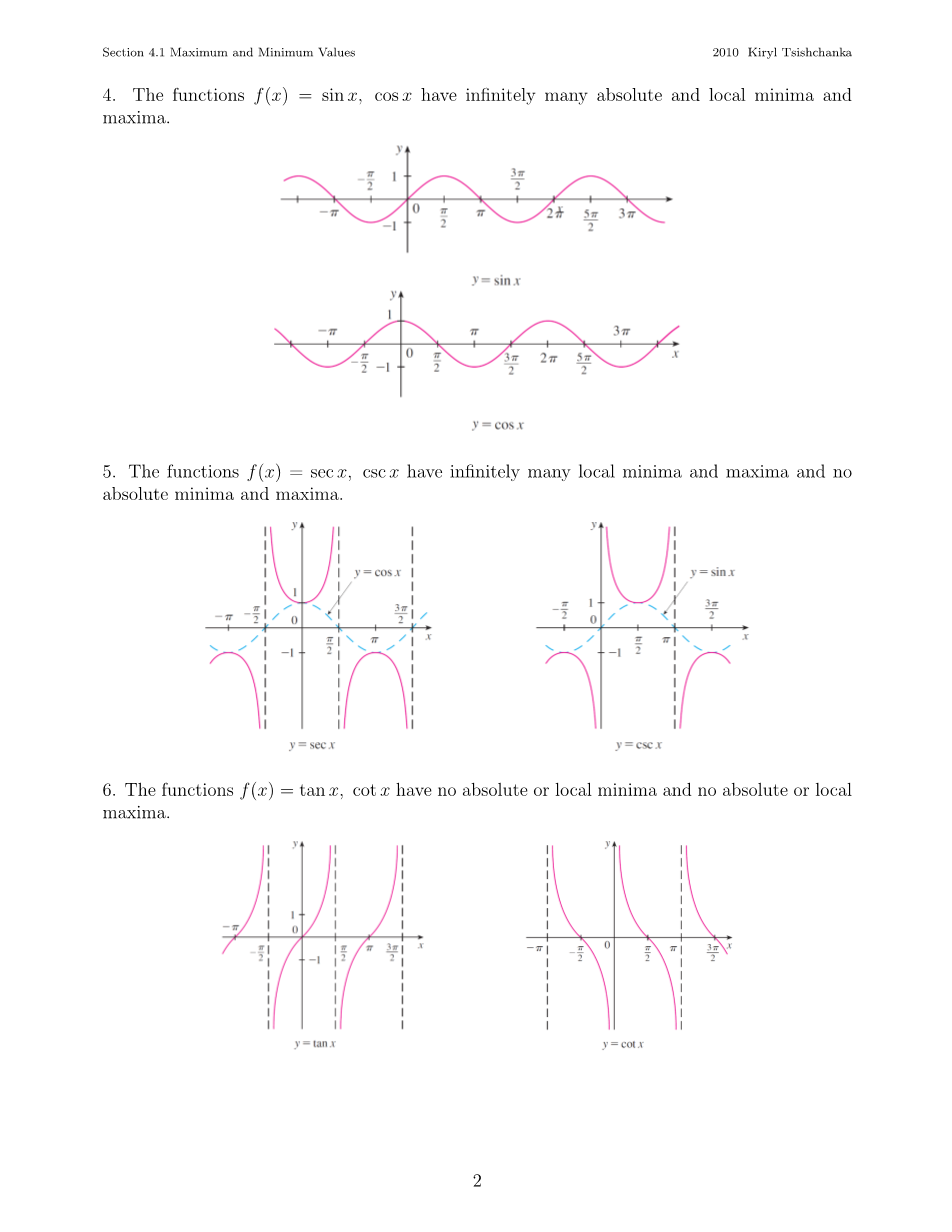
- 函数有无数多个最大值和最小值.
- 函数有无数多个局部最小值和最大值,但没有全局最大值和最小值.
- 函数都没有最大值和最小值.
- 函数在时取到绝对最小值且没有绝对最大值.同时函数在和时取到局部最小值和在时取到局部最大值.
- 函数在时取到绝对最小值,在时取到绝对最大值,函数没有局部最大值和最小值.
- 函数既没有绝对最大值和最小值,也没有局部最大值和最小值.
- 函数既没有绝对最大值和最小值,也没有局部最大值和最小值.
|
2 |
2 |
2 |
||||||
|
1 |
1 |
1 |
||||||
|
minus;2 minus;1 |
1 |
2 |
minus;2 minus;1 |
1 |
2 |
minus;2 minus;1 |
1 |
2 |
|
minus;1 |
minus;1 |
minus;1 |
||||||
|
minus;2 |
minus;2 |
minus;2 |
- 函数在每一点上都是最大值和最小值.
|
2 |
||||||||
|
1 |
||||||||
|
minus;2 minus;1 |
1 2 |
|||||||
|
minus;1 |
||||||||
|
minus;2 |
||||||||
定理(最值定理):如果函数在闭区间上连续,则存在,使得函数有绝对最大值和绝对最小值.
定理(费马定理):如果函数在点取到局部最小值或最大值,那么当存在时,.
注意1:这个定理的逆定理不成立.换句话说,当时,函数不一定有局部最小值或最大值.比如:如果函数,那么,当时,,但是这一点并不是函数的局部最大值或是最小值.
注意2:有时候不存在,但是是函数的一个局部最大值或是最小值.比如:如果函数,那么不存在,但是函数在时取到局部(和全局)最小值.
定义:一个函数的临界点是指在其函数的定义域内有一个点,它那么,那么不存在.
注意:从费马定理可知,如果函数在点取到局部最大值或是最小值,那么就是这个函数的一个临界点.
例如:
如果函数,那么,于是函数的唯一临界点是.
如果函数,那么,于是函数的唯一临界点是.
如果函数,那么,由于不属于函数的定义域,所以函数没有临界点.
例题:
找出函数的临界点.
找出函数的临界点.
解答:
我们有:
因此当时时,和.且所有点都存在,于是和是原函数的临界点.
我们有:
或者
简言之,
因此当时时,,解得;同时当时,不存在,此时.于是原函数的临界点为和.
例题:找出函数的临界点.
解答:我们有
简言之,
这里有另一种方法可以得到相同的结论:
或者
简言之,
.
因此当时时,,解得;同时当时,不存在,此时.于是原函数的临界点为和.
闭区间的方法:找出连续函数在闭区间上的绝对最大值和最小值:
- 找出函数在开区间上的临界点.
- 找出函数在区间两端点的函数值.
- 比较第一步和第二步的值,最大的就是函数的绝对最大值,最小的就是这个函数的绝对最小值.
例题:找出函数在区间上的绝对最大值和最小值,并指出在什么时候取到.
解答:
步骤1:由于
所以有两个临界点,它们分别是和.
步骤2:我们现在计算这个函数在临界点的函数值和两个端点的函数值.
我们有
,,,.
步骤3:最大值是55,最小值是23,因此原函数在上的绝对最大值等于55,在时取到,且绝对最小值是23,在时取到.
例题:
找出函数在区间上的绝对最大值和最小值,并指出在什么时候取到.
找出函数在区间上的绝对最大值和最小值,并指出在什么时候取到.
解答:
步骤1:由于
所以有两个临界点,它们分别是和.
步骤2:由于不属于区间内,所以我们现在只计算的函数值和两个端点和的函数值.我们有
,,.
步骤3:最大值是13,最小值是2,因此原函数在上的绝对最大值等于13,在时取到,且绝对最小值是2,在时取到.
步骤1:由于
所以有两个临界点,它们分别是和.
步骤2:现在我们要计算两个临界点所对应的函数值和两个端点和的函数值.我们有
,,,.
步骤3:最大值是9,最小值是,因此原函数在上的绝对最大值等于9,在时取到,且绝对最小值是,在时取到.
附加题
例题:找出函数在区间上的绝对最大值和最小值,并指出在什么时候取到.
解答:
步骤1:由于
所有原函数没有临界点.
步骤2:由于这个函数没有临界点,所以我们现在只要求计算两个端点和的函数值.
我们有
,.
步骤3:最大值是11,最小值是1,因此原函数在上的绝对最大值等于11,在时取到,且绝对最小值是1,在时取到.
例题:找出函数在区间上的绝对最大值和最小值,并指出在什么时候取到.
解答:
步骤1:由于
当时,,所以是原函数的临界点.
步骤2:现在我们要计算临界点的函数值以及两个端点和的函数值.
我们有
,
,
.
步骤3:最大值是11,最小值是,因此原函数在上的绝对最大值等于11,在时取到,且绝对最小值是,在时取到.
例题:找出函数在区间上的绝对最大值和最小值,并指出在什么时候取到.
解答:
步骤1:由于
当时,,所以是原函数的临界点.
步骤2:现在我们要计算临界点的函数值以及两个端点和的函数值.
我们有
,
,
.
步骤3:最大值是13,最小值是4,因此原函数在上的绝对最大值等于13,在时
剩余内容已隐藏,支付完成后下载完整资料
英语原文共 16 页,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[287012],资料为PDF文档或Word文档,PDF文档可免费转换为Word




