Monte Carlo方法的发展及其应用研究毕业论文
2020-04-23 20:05:00
摘 要
通用计算机的诞生,使得数值计算的能力大为增强。以此为背景下产生了Monte Carlo 方法,又叫随机试验方法。通过介绍 Monte Carlo方法的历史背景和目前的应用,说明Monte Carlo方法的广泛适用性。利用强大数定律说明了 Monte Carlo方法的可行性,依中心极限定理讨论了 Monte Carlo方法的误差和收敛速度。举例说明 Monte Carlo方法的几种抽样方法,并将其运用于定积分的计算。给出几种计算定积分方法,同时从抽样和随机数的产生两个方面改进后进行比较。
关键词:Monte Carlo方法 数值计算 强大数定律 中心极限定理
The Development and Application of Monte Carlo Method
Abstract
The born of the first general-purpose computer ENIAC greatly enhanced the ability of numerical calculation. A few years of development, Monte Carlo methods is widely used now, which is also called random testing method. By using the strong law of large numbers and central limit theorem to proof the feasibility and deviation of Monte Carlo methods. Several examples in different ways of the Monte Carlo methods for the integral calculation are given in order to discuss their difference.
Key Words: Monte Carlo Method; numerical calculation; the strong law of large numbers; central limit theorem
目录
摘要 2
ABSTRACT 3
目录 4
第一章 相关背景和发展应用 6
1.1 历史背景 6
1.2广泛应用 9
1.3发展现状 10
1.3.1马尔可夫链蒙特卡洛方法 10
1.3.2蒙特卡洛树搜索 11
第二章 基本原理 12
2.1逆变换法按照均匀分布抽样 12
2.2误差和收敛速度 17
第三章 Monte Carlo 方法在计算定积分的应用 19
3.1随机投点法计算定积分 19
3.2样本均值法计算积分 22
3.3积分算法的改进 25
第四章 讨论与总结 27
第五章 附录 29
1.在正方形区域内按均匀分布投点 29
2.随机投点法计算积分 29
3.样本均值法计算积分 30
4.计算重积分 30
4.重要性抽样 30
参考文献 32
致谢 33
第一章 相关背景和发展应用
1.1 历史背景
蒙特卡洛方法(Monte Carlo method),是一种以计算机程序进行统计模拟的计算方法,因此被称作统计模拟方法(statistical simulations)。Monte Carlo 方法的基本思想是通过简单随机抽样的模拟,得到近似的数值解。其核心观念就是利用事件发生的随机性,去解决实际上可以确定发生的问题。Monte Carlo 方法使用简单易于操作,在数学和物理上其他的计算方法难以起作用时,展示了强大的可行性。Monte Carlo 方法在最优化、数值积分和抽样统计这三类问题中普遍使用。
Monte Carlo 方法虽然是随着通用电子计算机的问世而出现,但是Monte Carlo 方法的思想原型最早的出现可以回溯至十七世纪末期启蒙时代的法国数学家,博物学家布丰(Georges-Louis Leclerc, Comte de Buffon)的投针实验,即向平行等距的木纹地板上随机投出长度小于木纹间距的短针,求短针落在两块地板之间与木纹相交的概率。布丰投针实验以几何概型作为其数学背景,向等间隔的宽度为 平行线之间随机投入 次长度为 的短线段,并要求 ,在短线段与平行线的 次相交中, 为短线段和平行线相交所成的锐角,如下图所示:
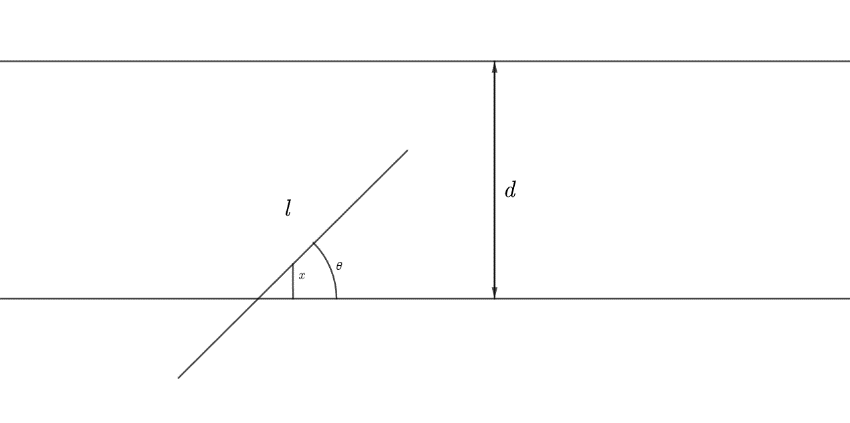
取线段的中点与两侧平行线之间的距离中较短的一个,由于投针的过程是随机性,可以认为 是服从区间上均匀分布的随机变量,并且 相互独立,而 即 。
当短线段与平行线相交时,存在以下关系:
按照均匀分布的概率密度函数,,投针问题中短线段与平行线相交的概率 变成在平面区域内满足上式的的区域 的面积与矩形面积 的比值:
分别计算平面区域 和 的面积:
结合两式,可近似得到 的一个近似值:
可以化简上述过程,采用跟为简单的方法近似计算 的值。在以单位长度为边长的一个正方形的区域内有一个相切的圆,则他们的面积比为 。在正方形区域内均匀投入一定数量的点,计算点到圆心的距离,用距离小于单位长度的个数和投入点的总数做比值,下图记录了从开始到 时程序运行后与真实值 之间的误差,运行附录中的程序得到下面的结果:
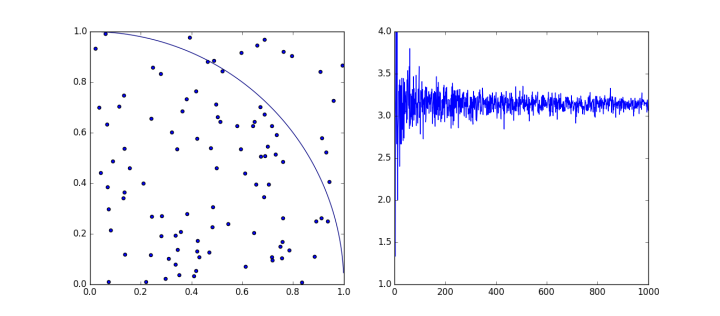
次数 | 结果 | 次数 | 结果 |
现代蒙特卡洛方法诞生于四十年代的制造核武器的曼哈顿计划(Manhattan Project),由冯诺依曼(John von Neumann)等人以摩纳哥的一处赌场命名。当时美籍波兰数学家斯坦尼斯拉夫·乌拉母(Stanislaw Ulam)正在高校任职同时参与洛斯阿拉摩斯国家实验室(Los Alamos National Laboratory)的核武器研究项目,在乌拉母首次应用马尔可夫链蒙特卡罗方法取得突破后,冯诺依曼立刻明白了这种方法的重要性,他对 ENIAC(Electronic Numerical Integrator And Computer,即电子数字积分机是第一台能够重新编程的通用计算机) 编程,使其可以通过 Monte Carlo 方法进行计算。1946年,洛斯阿拉莫斯国家实验室的物理学家们正在研究中子穿过各种材料是运动的距离。尽管当时他们已经通过计算得到了一些关键数据,比如中子与原子核碰撞之前在物体中走过的平均距离,以及中子在碰撞后将要释放的能量。但是他们仍然不能通过传统的确定性的数学方法解决所有的问题,在这个背景下乌拉母产生了通过多次随机试验解决问题的想法。当时乌拉母正在一场疾病的康复过程中,在一次单独玩甘菲德纸牌游戏(Canfield,游戏的目标是在四张基牌上形成四组牌点依次递增的完整同花顺)的过程中试图单纯的通过组合的计算来估计成功的概率。在花了很多时间计算后,他意识到不如玩一百次游戏,计算游戏结果中成功的次数,这样简单的解决方式可能比抽象的计算更加有效。在当时,电子计算机快速计算的能力已经得到广泛的应用。他当即联想到种子扩散问题,以及一些列相关的数学,物理问题。随后乌拉母与冯诺依曼描述了这个想法,并着手开始他们的工作。 鉴于当时需要保密的特殊要求,乌拉母和冯诺依曼对他们个工作取了 Monte Carlo 这个代号。可是当时产生随机数表的方法非常慢,对此冯诺依曼采用了一种新的产生伪随机数的方法:平方取中法(Middle-square method),它选择一个大数作为种子,计算这个大数的平方在得到新的数中取中间的和原来种子数位相同的数字作为新的种子。平方取中法并不是一种很好的方法,当时的科学家批评平方取中法过于粗暴,但是平方取中法还是凭借着能快速产生随机数的优势适用于 ENIAC。当时的计算工具能力非常有限使得其他的计算方法难以运行,Monte Carlo 方法称为了曼哈顿计划中模拟实验的核心。
1.2广泛应用




