带有凸非线性项的分数阶Laplace方程的解的对称性毕业论文
2020-04-25 19:40:42
摘 要
在这篇论文里,我们主要研究的是:带有凸非线性项的分数阶Laplace方程解的对称性。即,研究以下问题:
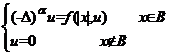 ,
,
解的对称性。参照文献[7]所使用的方法,先给出一个可以判断出对称性的命题,在此基础上我们再来证明我们所给出的结论。
本文分成四章,其布局如下:
第一章,我们将介绍我们这次研究的目的与意义,并介绍与论文相关的研究背景以及研究现状;
第二章,我们将会介绍一下在论文里我们所使用的方法,以及由该方法所得出的一些与我们这个课题相关的结论;
第三章,我们将会给出本次论文所得到的理论成果;
第四章,我们将会对我们的结论给出一个详细的证明,当然在此之前我们会做一些必要的工作,给出几个相应的引理。
关键词:分数阶Laplace方程 对称性 凸非线性 极大值原理 Hopf引理
ABSTRACT
In this paper, we mainly study the symmetry of solutions of fractional Laplace equation with convex nonlinearity. That is to say, the problem we study is:
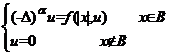 .
.
According to the method used in paper [7], we give a proposition that can judge the symmetry. Then we prove the conclusion we have given.
This paper is divided into four chapters, which are arranged as follows:
In the first chapter, we will introduce the purpose and significance of our research, and introduce the background and research status of related papers.
In the second Chapter, we will introduce the methods we used in this paper and some conclusions related to our subject.
In the third chapter, we will give the theoretical results of this paper.
In the last chapter, we will give a full proof of our conclusion. Of course, before that, we will do some necessary preparing to give some corresponding lemmas.
Key words: fractional Laplace equation、symmetry、 convex nonlinearity、maximum principle、Hopf lemma
目录
摘要 I
ABSTRACT II
第一章 引言 1
1.1 研究的目的及意义 1
1.2 背景介绍 1
1.3 分数阶Laplace方程的研究现状 2
第二章 所使用的方法及相关理论 4
2.1 预备知识 4
2.2 所使用的方法及相关理论 5
第三章 主要结论 6
第四章 理论证明 7
4.1 引理1、引理2及命题1 7
4.2 结论证明 12
参考文献 16
致谢 19
第一章 引言
1.1 研究的目的及意义
我们研究的目的是:探讨带有凸非线性项的分数阶Laplace方程的解是否具有对称性;若存在对称性,那么可能会具有什么样的对称性?对于这方面的研究,目前大家所熟悉的方法是移动平面法,但是我们总觉得移动平面法条件过于苛刻,于是我们希望可以找到一种方法能够在移动平面法不适用的情况下来研究分数阶Laplace方程解的对称性。我们的研究意义是:介绍一种研究分数阶Laplace方程解对称性的方法,使得在移动平面法失效的情况下使用这种方法可以得到分数阶Laplace方程解的对称性。
1.2 背景介绍
从微积分的产生以来,鉴于整数阶微积分有具体的物理意义,因此整数阶微积分在工程应用方面一直备受青睐。由于Laplace方程可以解释实际问题中的扩散现象,因此Laplace方程在很多邻域中都有着极广泛的应用,相关理论可参考[19-22]。但是随着社会的发展人们所需要解决的问题在逐渐的升级,Laplace方程的局限性也逐渐的暴露出来:整数阶Laplace方程解释不了反常扩散现象。
1695年L’Hopital在给Leibniz的信中,首次提出这样一个问题:当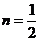 时,
时,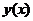 对
对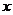 的
的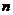 次导数所表示的是什么?也是在1695年,Leibniz写信给J.Beroulli,在信中也提到了任意实数阶导数的问题。这标志着分数阶微积分的诞生。从此以后,分数阶微积分开始缓慢地发展。
次导数所表示的是什么?也是在1695年,Leibniz写信给J.Beroulli,在信中也提到了任意实数阶导数的问题。这标志着分数阶微积分的诞生。从此以后,分数阶微积分开始缓慢地发展。
为了用数学的方法来解释反常扩散的问题,学者们尝试把整数阶Laplace方程推广到分数阶的情况。与此同时,随着生产实际的需要,学者们逐渐发现在许多物理模型中也发现了分数阶Laplace算子,例如Levy飞行、大幅振波、分子动力学等[3]。于是,各行各业的科研人员开始把他们的目光投向分数阶Laplace方程。此外,学者们还发现科学与工程中的非线性现象也可以用分数阶Laplace方程来描述。近年来,学者们甚至发现在金融领域的美式期权里也存在分数阶Laplace方程[23]。为了用分数阶Laplace方程解决实际问题,学者们迫不及待地想要了解分数阶Laplace方程所具有的性质。在国内外学者们的努力探索下,我们发现整数阶Laplace方程有非常良好的性质并且这些性质容易观察出来,于是我们希望分数阶Laplace方程也能保持这些性质。然而事情并非我们想象的那么简单,分数阶Laplace方程似乎并没有继承这些性质。于是为了掌握分数阶Laplace方程所具有的性质,学者们开始从不同的角度来分析、探讨满足一定条件的分数阶Laplace方程。由此,数学的分支如泛函分析、实变分等也逐渐地发展起来[17][18]。
经过深层次、多角度的分析,学者们得到了这样一个结论——分数阶Laplace算子有局部性和非奇异性的特点,这与经典的Laplace算子有着本质的区别。
1.3 分数阶Laplace方程的研究现状
在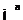 空间里(
空间里(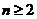 ),分数阶Laplace算子为:
),分数阶Laplace算子为:




