二维五角结构过渡金属硫系化合物的电子结构研究毕业论文
2020-02-18 10:32:07
摘 要
石墨烯的发现引起了二维材料研究的热潮,然而石墨烯的零带隙问题限制了其在电子逻辑器件方面的应用。而与之类似的以MoS2为代表的2D过渡金属硫系化合物(TMDCs)则因其特殊的能带结构、半导体或超导性质以及优秀的机械性能等,在纳米工程和光电器件方面具有广阔的应用前景。我们知道,TMDCs典型的结构是六角相(hexagonal),然而PdSe2/PdS2等却能形成独特的五角相(pentagonal)结构。为什么会有五角相的出现,这种五角相又将带来哪些性质上的改变,自然也引起了人们的关注。本文将通过第一性原理计算探究这种独特结构的光学性质、能带结构,并与六角相TMDCs、四六主族IVX2(IV=C,Si,Ge,Sn,Pb;X=S,Se,Te)型五角相化合物作对比研究,考察penta-TMDCs的独特之处以及应用前景。
关键词:TMDCs,五角相pentagonal,光学性质,能带结构
Abstract
The discovery of graphene has caused a boom in two-dimensional materials research, but the zero band gap problem of graphene limits its application in electronic logic devices. Similar to the 2D transition metal-sulfur compounds (TMDCs) represented by MoS2, they have a wide range of nano-engineering and optoelectronic devices due to their special band structure, semiconductor or superconducting properties, and excellent mechanical properties. Application prospects. We know that the typical structure of TMDCs is hexagonal, but PdSe2/PdS2 can form a unique pentagonal structure. Why is there a appearance of the pentagonal phase? What kind of changes in the nature of this pentagonal phase will naturally attract people's attention. This paper will explore the optical properties and band structure of this unique structure by first-principles calculations, and with hexagonal phase TMDCs, four or six main groups IVX2 (IV=C, Si, Ge, Sn, Pb; X=S, Se , Te) pentagonal phase compounds for comparative study, to examine the uniqueness and application prospects of penta-TMDCs.
Key Words:TMDCs, pentagonal, optical properties, band structure
目录
第1章 绪论 1
1.1 研究背景 1
1.2 本文思路与工作要点 3
第2章 理论基础 4
2.1 第一性原理与多电子体系薛定谔方程 4
2.2 三种近似方法 4
2.2.1 Born-Oppenheimer近似 4
2.2.2 Thomas-Fermi- Dirac近似 5
2.2.3 Hohenberg-Kohn定理 5
2.3 CASTEP自洽求解过程 6
2.4 交换关联泛函 8
2.4.1 局域密度近似LDA 8
2.4.2 广义梯度近似GGA 8
第3章 五角相过渡金属硫系化合物计算分析 10
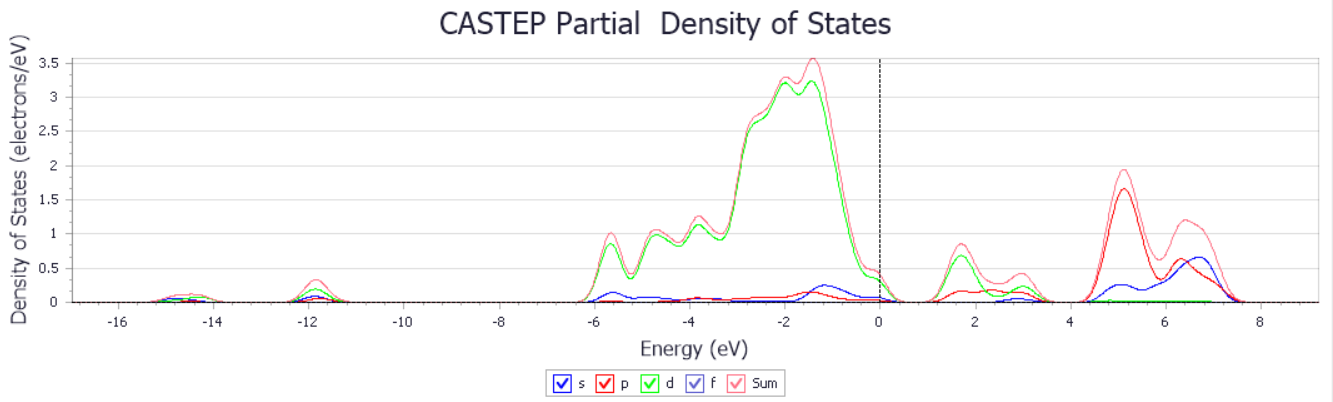
3.1 PdSe2计算分析 11
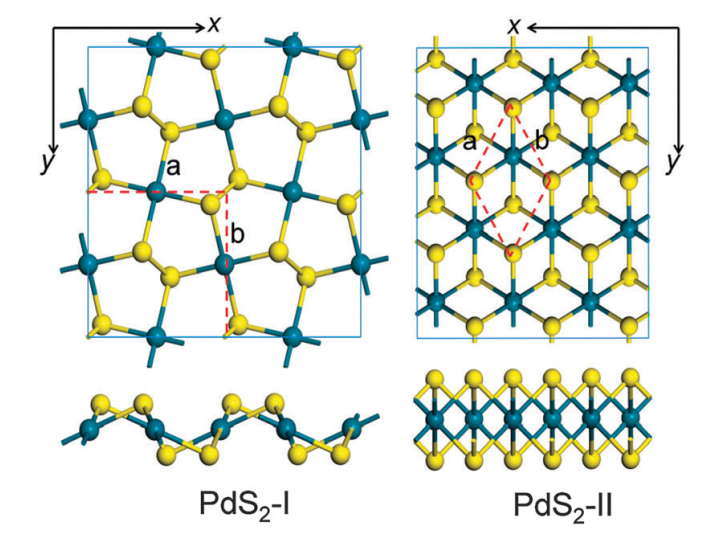
3.1.1 PdSe2的几何结构 11
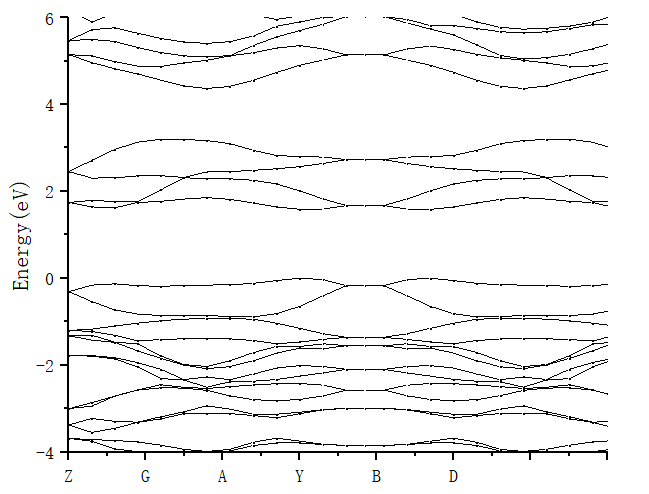
3.1.2 PdSe2的电子结构 12
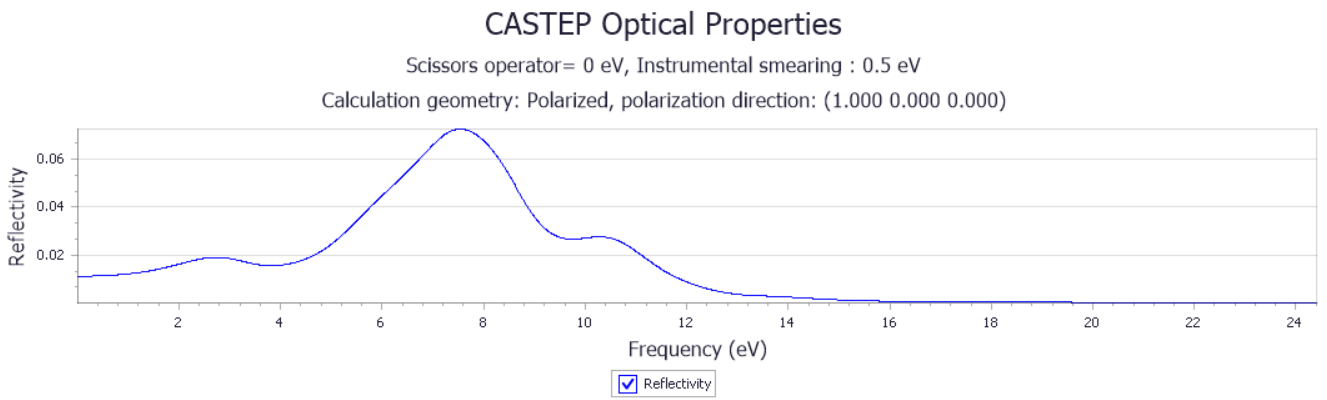
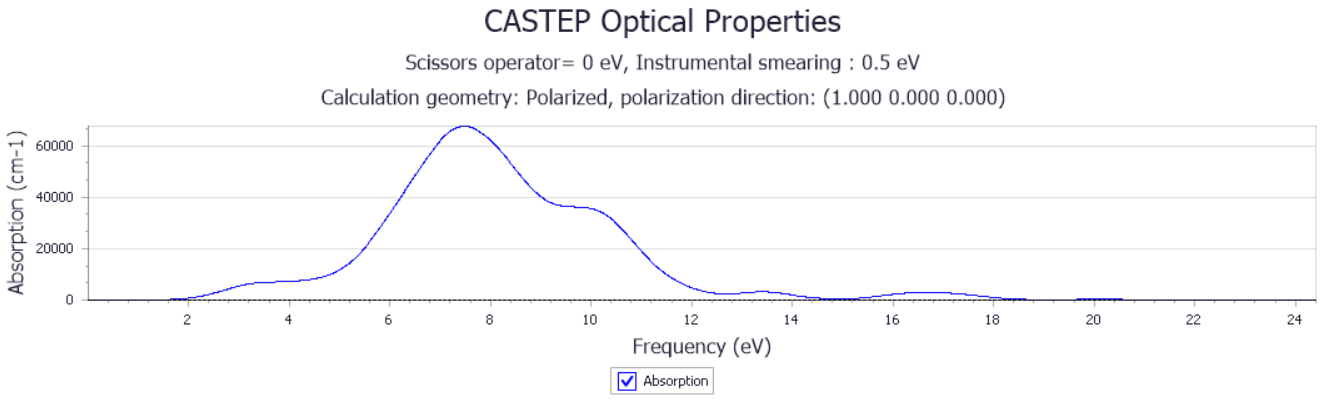
3.1.3 PdSe2的光学性质 13
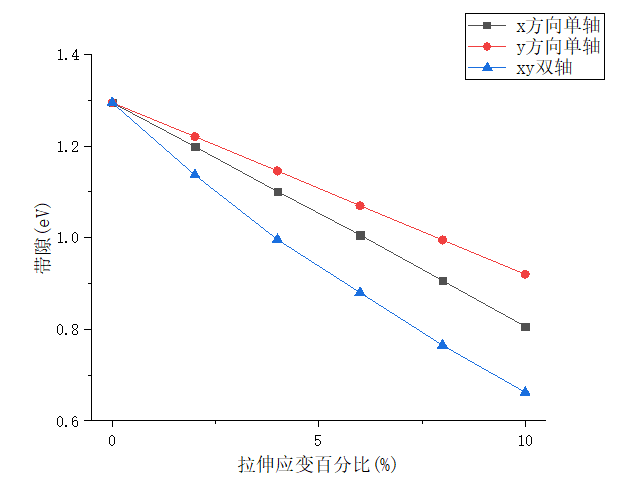
3.1.4 PdSe2的拉伸改变 15
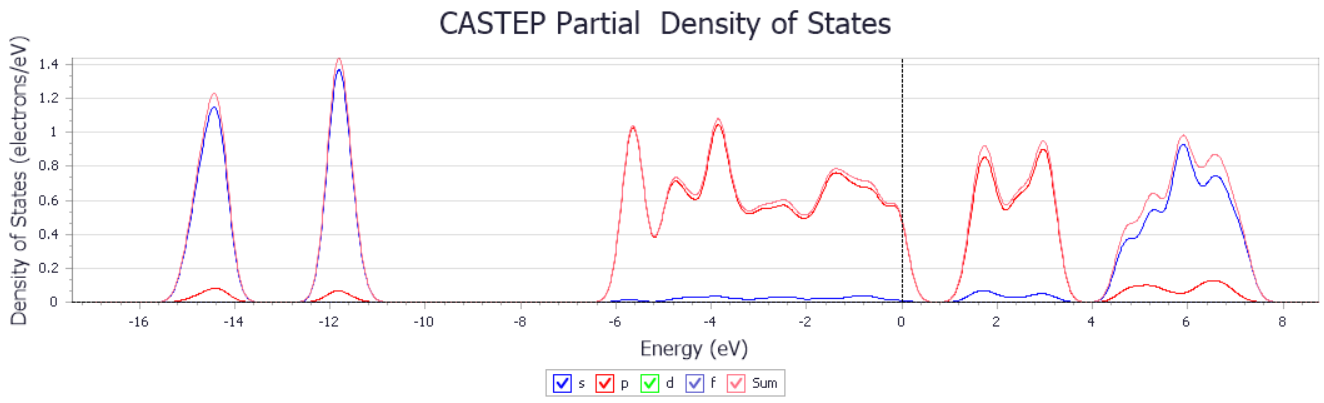
3.2 PdS2计算分析 15
3.2.1 PdS2的几何结构 17
3.2.2 PdS2的电子结构 18
3.2.3 PdS2的光学性质 19
3.2.4 PdS2的拉伸改变 20
第4章 五角相过渡金属硫系化合物与类似材料对比 21
4.1 四六主族二维五角相 21
4.2 块体五角相 21
4.3 六角相过渡金属硫系化合物 22
第5章 总结与展望 24
参考文献 25
致谢 27
第1章 绪论
1.1 研究背景
去年三月,麻省理工学院的在读博士生曹原以第一作者身份在《nature》上发表了两篇重磅论文,揭示了“魔角”下石墨烯的超导性质:以1.1°放置相互平行的石墨烯层时,体系会产生超导现象。然而,石墨烯的价带和导带相交于First Brillouin Zone的六个顶点,故而石墨烯是一种零带隙的二维半导体材料,这一特点也限制了它在电子逻辑器件方面的应用。
于是,人们转而探索类石墨烯材料:二维过渡金属硫族化合物 (Transition Metal Dichalcogenides, TMDCs)。TMDCs作为一种全新的类石墨烯材料,具有优异的电学、光学及催化特性[1],这源于其能带结构中的维度效应和电子调制[2],可用于逻辑器件[3]。由于TMDCs带隙可调,它可以用于场效应晶体管和逻辑器件,这方面有着优于石墨烯的特性,例如CdS,PdS等[4]。以MoS2为例,块体MoS2为间接带隙半导体,带隙宽度1.29 eV;随着层数的减少,带隙逐渐变大并发生间接带隙到直接带隙的转变,最终得到1.8 eV的直接带隙[5]。随着应用原子材料的不同,如MoS2、MoSe2、WS2、WSe2、NbS2等[6],其将具有半导体、金属态、超导性质等,这便使得TMDCs在纳米电子器件和光电子学等诸多领域具有广阔的应用前景,从而受到广泛的关注。
TMDCs的结构与石墨烯类似:每一层结构的厚度为6~7 埃,它们由六方层状金属原子三明治式地包裹在两层硫族原子中。单层内部是共价键,而层与层之间则通过较弱的范德瓦尔斯力连接着,因此这就使它可以沿着层的表面撕开。在制备方面,TMDCs的制备技术包括分子束外延(MBE),化学气相沉积(CVD),有机金属化学气相沉积(MOCVD)等。而二维单层TMDCs的获得方法与石墨烯相似,典型的便是机械剥离法。石墨烯的机械剥离法又称为苏格兰胶带法,没有任何化学掺杂,对于材料纯度的维护很有帮助,其得到的二维材料的性质测试准确。而对于过渡金属硫化物,相较于高温液相法[7],因为其层与层之间弱小的范德瓦耳斯力作用,机械制作的难度也随之下降,所以机械剥离也是最热门可靠的2D-TMDCs制作方法。但这种方法也有非常明显的缺陷,例如制备的薄膜厚度和尺寸不可控,由于机械方法会被撕裂,得不到完整的结构,对于边缘态的分析非常不利,另外机械剥离的产量低,制作手法的繁杂导致重复性较差[8]。
如前所述,一般TMDCs的典型结构是六角相(hexagonal),不过PdSe2/PdS2等却能形成独特的五角(pentagonal)结构。那么这种独特的结构会带来什么奇特的性质,其他TMDCs又是否具有这种Pentagonal结构便成了值得探讨的话题,这也正是本文所要研究的问题。具体以PdSe2为例,每个Pd原子与同一层中的四个Se原子结合,两个相邻的Se原子可形成共价的Se-Se键,两个Pd原子和三个S原子可形成皱褶五角形[9]。块体PdSe2在具有空间群Pbca的PdS2型斜方晶结构中结晶,块体结构由沿c轴堆叠的2D Se-Pd-Se层组成,它们彼此很好地分开,具有明显的范德华间隙。每个单层具有三层构造,其中间的Pd原子与位于顶层和底层的四个Se原子共价键合。此外,Se-Se键合连接顶层和底层,这种布置平面的分离较大。在计算中,通过沿着轴线添加真空空间从单个结构中切出单层结构,这使得平面中的潜在各向异性成为可能[10]。另外,二维高温铁磁材料在自旋电子方面也有重要应用。通过从分层散装材料中剥离,可制成高度空气稳定的PdSe2单层半导体。这种优异的非磁性单层半导体非常有希望实现稳健的铁磁性,甚至半金属铁磁性(100%自旋极化)。第一性原理研究表明,PdSe2单层可以达到Stoner铁磁性,最大居里温度达到800K,铁磁性的空穴浓度阈值随着单轴应力的增加而降低。此外,在一些空穴浓度区域中可以实现半金属化。对于10%的应变(单轴拉伸应力为4.4 N / m),单层可以达到150 K的半金属铁磁性。磁各向异性能量不仅适用于稳定2D铁磁性而且还适用于实现快速磁化反转。还可以通过施加横向单轴应力来控制磁化。具有这些优点的高度空气稳定的PdSe2单层非常有望用于自旋电子应用[11]。
另一种新型的2D五边形NbX(penta-NbX,X = S,Se或Te)单层系列也具有良好应用前景。这些新材料对机械应变,晶格动力学和热波动是稳定的,因为这些材料中Nb和X元素之间存在离子和共价键。随着X从S 、Se变为Te,penta-NbX从金属变为半导体。penta-NbTe是一种直接带隙半导体,有着极高的载流子迁移率。由于金属五氮杂硼化合物在很宽的氢气覆盖范围内具有较低的过电位,它还可能用于析氢反应。可以预见,penta-NbX单分子层可能在电子和电催化中得到应用[12]。
还有学者从理论上设计了具有五边形结构和超高载流子迁移率的二维材料,以及通过第一原理计算和k·p模型预测从节点线半金属转变到五角结构硫族化合物中的大间隙量子自旋霍尔态[13]。非常有希望在具有适度带隙的二维(2D)原子晶体中达到高载流子迁移率以用于电子应用。在这项研究中发现的两种二维半导体材料penta-PdX2(X = P,As)是实现这一目标的强力候选者。penta-PdP2和penta-PdAs2都具有0.7-0.8eV的带隙。它们的载流子迁移率对于电子来说高达 ,对于空穴来说是 ,是这类2D半导体中最高的。此外,通过应用双轴应变可以有效地调节有效质量和带隙。电子有效质量首先攀升,然后在拉伸载荷下大幅下降,penta- PdP2的转折点为5%,PdAs2的转折点为2%。此外,penta-PdX2单层在宽波长范围内表现出较强的光吸收。所有这些出色的性能使penta-PdX2成为超快速电子和光电应用的有希望的候选者[14]。
可以预见,penta-TMDCs作为一种重要的半导体材料[15],凭借着更优于石墨烯的特性[16],将在场效应晶体管、逻辑电路、传感器、微波吸收和催化等领域产生重要的应用。
1.2 本文思路与工作要点
基于以上背景,本文工作将是研究独特五角结构TMDCs,参照Yuan Hao,Li Zhenyu,Yang Jinlong等人的工作[14],从理论计算上分析能带结构、光学性质、拉伸应变等,希望拓展研究前景与市场应用。
具体来说,第2章将简述本文的计算原理,主要涉及密度泛函理论(DFT)的简介、三种近似方法,主要计算软件CASTEP的自洽求解过程,影响到计算精度的近似方法的对比分析。在第3章中,本文将具体计算分析两种二位五角相过渡金属硫系化合物(penta-TMDCs),penta-PdSe2和penta-PdS2的各种性质,如能带结构、光学性质、应变拉伸作用等。在第4章,我们将简单介绍几种类似的材料,主要是四六主族penta-IV X 2(IV= C, Si, Ge, Sn, Pb; X=S, Se, Te) 的二维五角相化合物,以PbSe2为例;块体五角相TMDCs,以NiSe2和NiS2为例;六角相TMDCs,以MoS2为例。根据第3章的结论,将penta-TMDCs与这几种材料做一个对比,以期了解它的独特之处,并尝试分析成因、预期可行的研究方向及性质。在最后的第5章中,我们将会做一个总结,并探讨一下penta-TMDCs的应用前景。
第2章 理论基础
2.1 第一性原理与多电子体系薛定谔方程
依据量子力学理论,以及电子和原子核之间的相互作用原理和基本运动规律,经过某些近似方法的变动后直接求解薛定谔(Schrödinger)方程的方法,通常称之为第一性原理 (The first principle)计算。我们知道电子和原子核组成了原子,原子组成了分子,分子再组成物质。量子力学计算就是根据这之间的相互作用原理去计算分子的空间分布结构和体系能量值,之后再进一步得出体系的其他物理化学性质。这种方法很好地“第一手”获得分子的空间结构和相对应的各种物理性质,具有直接性和第一性,这样的计算理论自然就称为第一性原理了。
由于固体材料的许多基本物理性质与材料的电子性质有着极大的关联,或者说基本的物理性质就是由其微观的电子结构决定的,那么通过求解多粒子体系的Schrödinger方程来求解电子结构进而得到基本物性就变得可行而重要了。通常而言,固体材料可以视为原子核及其周围电子组成,则量子力学中的Schrödinger方程可以表示为:
其中等式右边五项分别为电子的动能项、原子核的动能项、电子与电子的相互作用项、核与核的相互作用项、电子与原子核的相互作用项。显然,由阿伏伽德罗常数我们知道,每立方米物质所包含的粒子数是十分巨大的,这对应着的i,j求和指标也会高达10的29次方量级,故而需做一定近似。对此,我们一般有三种近似方法。
2.2 三种近似方法
2.2.1 Born-Oppenheimer近似
我们知道,质子的质量为1.6726231×10-27kg,中子的质量为1.6749286×10-27kg,电子的质量为9.1093897×10-31kg[17]。由这几个数据可以直观地看出,质子和中子的质量都远大于电子,由质子和中子构成的原子核的质量也将比电子高三个数量级以上,这使得原子核的速度比电子慢得多,电子的驰豫时间比原子核的驰豫时间要小上三个数量级。鉴于上述事实,我们可以将系统分为两个部分来考虑:分析核的运动时忽略电子的详细布局情形,分析电子运动时则假定原子核静止于原位置不动。这样就能将原子核与电子分离求解。
哈密顿量:
2.2.2 Thomas-Fermi- Dirac近似
托马斯和费米的近似理论不考虑电子的相互作用,将这部分视为没有相互作用的均匀电子气,并用电子密度的函数来表达系统的动能。上世纪三十年代,狄拉克又利用局域密度近似来处理这之间的关联关系,发展了这一近似理论。他将外场下的能量方程表示为:
但是这种理论方法也放弃了原子壳层信息等性质的描述。
2.2.3 Hohenberg-Kohn定理
定理一:粒子数密度函数是一个决定系统基态物理量性质的基本变量。
根据这一定理不难推出,基态的电荷密度实际上确定了这一个体系的哈密顿量,体系的所有波函数也都跟着被唯一决定了,那么系统的所有性质可以由基态密度函数来确定。实际上,对于多电子体系,
我们假定基态电荷密度为,它对应有不一样的外场和,相对应的哈密顿量分别为和,基态波函数分别为和。因为不是的基态,则:
同时,
那么,
同样,
最后推出:
这显然是不成立的,所以系统的所有性质应当由基态密度函数唯一确定。
定理二:粒子数固定时,能量泛函对密度函数的变分给出系统基态的能量值。
实际上,电荷密度决定体系的所有性质,那么我们可以将系统的能量定义为电荷密度ρ(r)的泛函。由变分原理可知,系统的基态能就是能量泛函在粒子数固定时的最小值,对应也正是基态的电荷密度分布。我们将这样一个能量泛函表示为:
其中,
根据定理一,
根据变分原理有:
显然,基态电荷密度给出的能量才是最低的。
2.3 CASTEP自洽求解过程
依据上述霍恩伯格-科恩(Hohenberg-Kohn)定理,我们可以将泛函写成单电子波函数的形式,这些泛函在整体上定义了电荷密度:
表达式中出现两倍的系数因子2是因为电子具有自旋,而且泡利不相容原理指出,每一个单电子波函数能够被不同自旋的两个电子所占据,当然这是纯粹的量子力学情形。我们再将能量泛函写为:
这个表达式的意思是将泛函写成具有简单解析形式的一项,以及其他部分。其中第一个已知项主要包括四个方面的贡献,即:
上式右侧四项分别是电子的动能、电子与原子核之间的相互作用、电子之间的相互作用、原子核之间的相互作用。而能量泛函表达式中的另一项则是交换关联函数,定义的是前一项以外的相关量子力学作用。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: