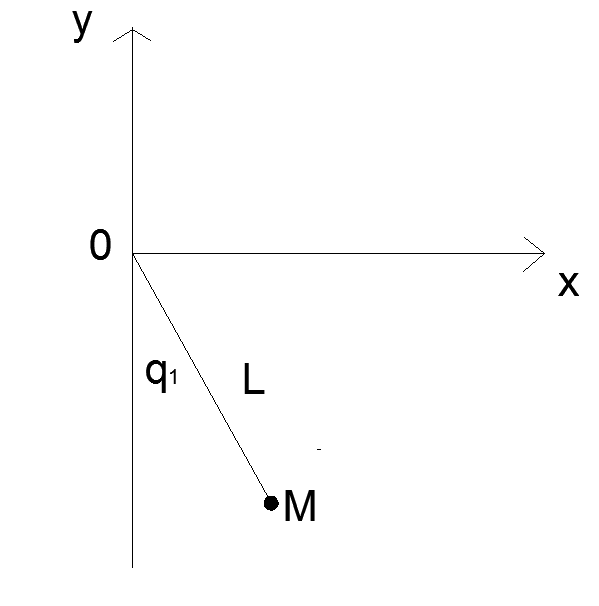摘 要

随着时代的进步，各个领域都能看到机器人技术的身影。如航天、医疗、勘探等等。其中机械臂的建模与控制是重要的研究话题之一。如今，机械臂的建模已十分简单，但就控制方法还有很大是研究空间。随着工业化的不断深入，刚性机械臂的控制方法已不能满足人们的要求，柔性机械臂的控制方法逐渐走入人们的眼帘。

本文以单连杆机械臂为研究对象，利用拉格朗日方程推导了单连杆机械臂的动力学方程，提出状态反馈的方法设计控制器。用近似线性化方法和精确线性化得到单连杆机械臂的线性数学模型，并设计控制器，然后用simulink软件进行仿真。接下来为单连杆机械臂设计有限拍控制律，对象为近似线性化模型，并仿真实现，然后与精确化线性对象所设计的控制系统仿真结果作比较。最后提出单连杆机械臂基于齐次系统的有限时间状态反馈镇定方法。

关键词：机械臂；近似线性化；精确线性化；有限时间控制；系统仿真；

李雅普诺夫稳定性

Abstract

With the progress of the times, all areas can see the robot technology figure. Such as aerospace, medical, exploration and so on. The modeling and control of the manipulator is one of the important research topics. Nowadays, the modeling of the manipulator has been very simple, but there is still much room for the control method. With the deepening of industrialization, rigid arm control methods can not meet the requirements of people, flexible mechanical arm control method gradually into the people's eyes.

In this paper, the single-link manipulator is used as the object of study, the dynamic equation of the single-link manipulator is deduced by using the Lagrangian equation, and the method of state feedback is proposed. The linear mathematical model of the single - link manipulator is obtained by the approximate linearization method and the linearization of the single - link manipulator. The state feedback controller is designed and then simulated by simulink software. Then, the finite control method is designed for the single-link manipulator, and the object is an approximate linearization model. The simulation results are compared with the simulation results designed by the precise linear object. Finally, a finite time state feedback stabilization method for single - link manipulator based on homogeneous system is proposed.

Keywords：Mechanical arm；Approximate linearization；Precise linearization；finite-time control；system simulation；Lyapunov stability

目录

摘要 I

Abstract II

第一章 绪论 1

1.1引言 1

1.2本文的研究目的及意义 1

1.3机械臂国内外研究现状 2

1.4机械臂动力学建立模型方法的综合概述 3

1.5机械臂控制方法综述 4

1.6本文研究内容 5

第二章 单连杆机械臂系统的建模 6

2.1机械臂动力学建模 6

2.1.1有势力拉格朗日函数的介绍 6

2.1.2机械臂动力学建模综述 7

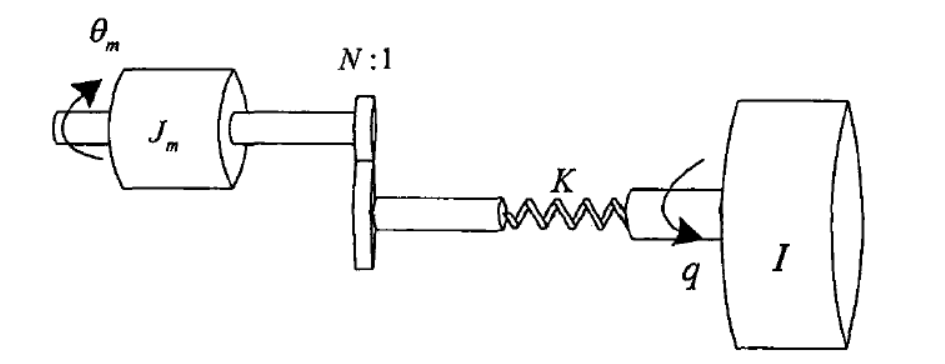
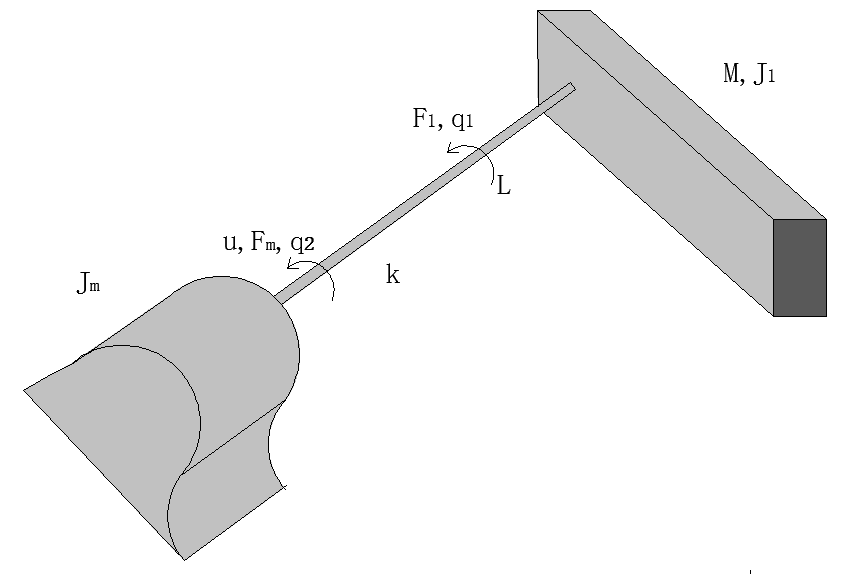
2.2单连杆机械臂的组成 8

2.3基于拉格朗日方程的单连杆机械臂的动力学建模 9

2.4 simulink软件介绍 11

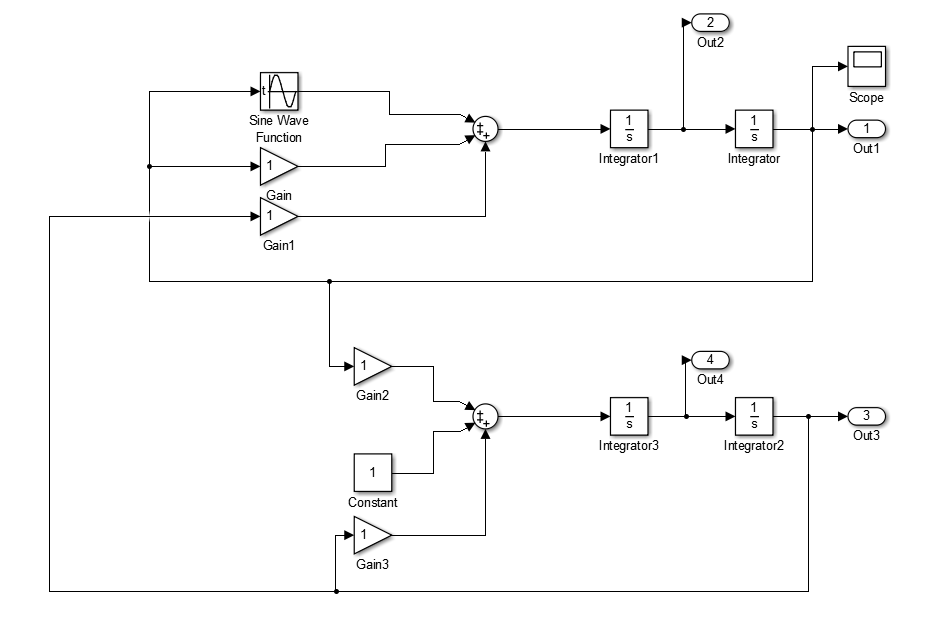
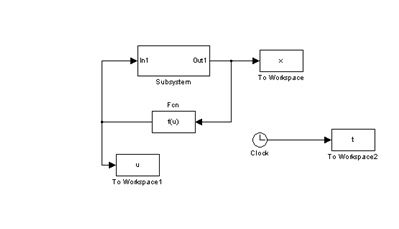
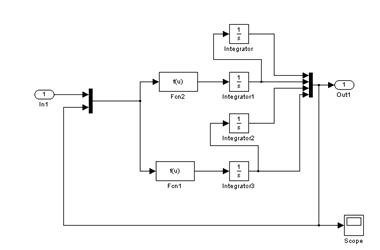
2.5单连杆机械臂在simulink环境下的建模 12

第三章 单连杆机械臂稳定控制与仿真的实现 13

3.1基于近似线性化状态反馈控制器 13

3.1.1单连杆机械臂数学模型的近似线性化 13

3.1.2 基于近似线性化模型的状态反馈控制器设计 13

3.1.3仿真实验 15

3.2 基于精确线性化模型的状态反馈控制器 18

3.2.1 单连杆机械臂机械臂数学模型的精确线性化 18

3.2.2 基于精确线性化模型的状态反馈控制器设计 19

3.2.3仿真实验 20

第四章 有限时间控制器的设计及仿真实验 23

4.1有限拍时间控制器设计及仿真实现 23

4.1.1有限时间控制简介 23

4.1.2有限拍时间控制器设计 23

4.1.3仿真实验及数据对比 25

4.2基于齐次系统方法的有限时间控制器的设计 29

第五章 总结与展望 33

第一章 绪论

1.1引言

从上个世纪机械臂问世以来，机械臂已给人们的生活产生了深远的影响，在时代的发展下，技术的革新中，机械臂的研究也成为热门话题之一，其应用范围也逐渐涵盖各个领域，遍及工业、勘探、航天、医学治疗、国家防御系统等各个领域^[1]。机械臂的优势在于可以不间断的工作，去人类无法达到的领域如太空、深海工作等等。图1-1机械臂的应用实例。

图1-1 机械臂在工业生产上的应用 图1-2 机械臂在医学治疗上的应用

1.2本文的研究目的及意义

从第一台机器人问世以来，机器人技术有了质的飞跃。而机械臂作为其重要的分支，也有了巨大的发展。机械臂是一类可以模仿人类动作、并且可以自主完成生产的设备。对提高生产效率，改善劳动环境有巨大的帮助，同时也具有操作灵活，耐用性好，以及精度高等优点^[2]。

随着时代的需求变化，机器人技术也愈发成熟。对具有高性能的机器人、机械臂的研究也成为热点。对于刚性机械臂的研究，人们取得了一定的成果^[3]。但是其控制方法很难达到现代工业所要求的精度，因此，此理论被延伸，发展。所以本文针对单连杆柔性机械臂进行建模并用设计控制器。

1.3机械臂国内外研究现状

国外机械臂最初是在1950s从美国开始研究的。日本、欧洲、俄罗斯的研究工作大概比美国晚了10年。目前机械臂已实现了商品化，工业机械臂的厂家很多，具有代表性的有：ABB、莫托曼、Adept、川崎、ＤＥＮＳＯ和发那科等等^[4]。　

下面介绍几款机械臂的代表：

如图1-3，它是由法国Cybernetics公司设计的排爆机械臂，具有6个自由度，装有内置望远镜的机械臂长达2.8m，有效荷载30kgf。采用的控制系统是四象限控制系统，能在运动过程中完成各类操作^[5]。

图1-3 排爆机械臂 图1-4 斯坦福手臂

如图1-4，它是由美国斯坦福人工智能实验室所设计的，具有6个自由度，由PDP-6的数字装置控制，有一个棱镜和五个旋转关节。由直流电动机驱动，同时配有电位机。

如图1-5，它是由日本山梨大学所研制的柔顺装配机械臂，它是一种里程碑式的机械臂，因为它所采用的四轴低成本设计完美的适应了小部件的装配^[6]。节约成本，方便操作。

图1-5 山梨大学柔顺装配机械臂

我国在应用轻型机械臂上起步较晚，如图1-6是沈阳自动化研究所研制的“灵蜥-h”反恐防爆机械臂 ，它具有6个自由度，最大伸展抓重为5千克，工作时最大高度可达2.2m^[7]。

图1-6 “灵蜥-h”反恐防爆机械臂

如图1-7，它是由北京邮电大学开发的六自由度机械臂，采用Kane方法建模，奇异摄动控制，提高了控制精度^[8]。

图1-7 六自由度机械臂

1.4机械臂动力学建立模型方法的综合概述

机械臂动力学建模方法主要有Newton-Euler方程、Lagrange方程、Kane方程、变分原理、虚位移、哈密尔顿原理和神经网路逼近法。基本上是通过对物体的状态进行列式计算，得到系统的力，转动惯量和加速度三者的关系，在通过相关理论公式的运算，得到系统的动力学方程。

下面介绍两个主要理论：

Newton-Euler方程

其基本定理是牛顿第二定律，通过建立系统内各个物体的运动状态的方程来描述机械臂。但是对于多自由机械臂，利用牛顿力学确立其动力学方程就十分困难。

Lagrange方程

通过建立广义坐标来描述系统的状态，并对时间微分，计算系统的动能、势能和虚功，在通过推导，从建立方程。

1.5机械臂控制方法综述

基本控制方法：确定系统的结构与各项参数之后，用方程或者不等式作为模型来描述系统的动态特性。但是由于机械臂是非线性和不确定系统，所以这种方法很难达到控制要求。

PID控制：采用此控制方式易于实现控制，也不需要建立模型，只需要知道系统动力学方程即可。此方法缺点太明显，系统不稳定，夏小平用此方法设计过控制器。

自适应控制：通过对比自身性能与要求性能来修改性个组件参数，从而使系统处于最佳状态，缺点是计算复杂，对实时性要求很高。韩正等人用此方法取得了不错的成果。

鲁棒控制：保证了不确定系统的稳定，只需要知道不确定参数的阈值^[9]。黄琳用此控制取得了较好的成果。

模糊控制：控制器主要由模糊器、模糊规则库、模糊推理机、解模糊器组成，具有高度非线性映射逼近能力^[10]。崔玲丽等人设计了单连杆机械臂的模糊神经控制。

变结构控制：不连续的非线性控制，由于滑动模块的设计可以忽略系统参数和扰动，所以其响应所需时间短，抗干扰能力强^[11]。范猛、李丹等人设计了基于此方法的双连杆机械臂。

1.6本文研究内容

本文以单连杆机械臂作为研究对象，建立其动力学模型，设计合理的控制器，达到预期效果

论文章节安排如下：

第一章，简单说明了本文的研究目的及意义，并介绍机械臂的国内外发展现状，简要介绍了机械臂的建立模型方法，以及控制方法。

第二章，利用Lagrange原理建立单连杆机械臂的动力学方程并用simulink软件对其建立模型。

第三章，对单连杆机械臂设计稳定控制器，利用近似线性化和精确线性化方法建模并设计状态反馈控制器以及仿真，达到理想的结果。

第四章，以近似线性化模型为对象，提出了有限拍控制律，并设计控制器，并与精确线性化的模型所设计的控制器相比较，最后提出一种基于齐次系统方法的有限时间控制器。

第五章，总结与展望。

第二章 单连杆机械臂系统的建模

2.1机械臂动力学建模

2.1.1有势力拉格朗日函数的介绍

涉及到广义坐标和自由度，k个自由度的质点系统，系统的约束是理想化的，那么系统的广义坐标可以定义为q₁、q₂、...、q_k，，各个质点的r_i就可以用广义坐标与时间之间的关系来表示。

Lagrange方程由广义坐标对时间的一阶和二阶导数组成，其形式如下：

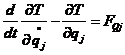（2-1）

其中动能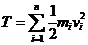

相关图片展示：