摘 要

旅行商问题（Traveling Salesman Problem，TSP）是车辆路线问题（Vehicle Routing Problem，VRP）的特例，已经证明旅行商问题是典型的NP完全问题，而多旅行商问题（Multiple Traveling Salesman Problem，MTSP）是旅行商问题的扩展，更加符合实际优化问题对应的模型，因而具有较高的理论研究和应用价值。

本文借助数学软件MATLAB，首先针对多旅行商问题应用标准遗传算法（SGA），模拟退火算法（SA）来求解,接着对这两种算法的仿真结果进行了比较分析，所得结果对于优化求解多旅行商问题具有重要的指导意义。

基于上述所用算法的结果探讨，论文主要研究了改进单亲遗传算法（IPGA）和多染色体遗传算法（MCGA）来求解多旅行商问题。其中IPGA采用了单亲遗传思想，无法使用双亲交叉操作，编码方法采用两部分染色体表达方式，选择操作使用分组精英选择策略。有针对性地提出了四种变异策略，变异操作采用四种变异策略之间的选择性组合，消除了变异概率。MCGA则采用了多染色体编码方式。

MATLAB实验过程中，将采用SGA、IPGA、MCGA和SA实现的程序进行了仿真对比，结果表明，针对同一多旅行商问题模型，IPGA和MCGA能够有效地解决多旅行商问题，MCGA具有可靠的近似解，IPGA运算效率更高。

关键词：多旅行商问题；遗传算法；模拟退火算法；单亲遗传

Abstract

The traveling salesman problem (TSP) is a special case of the vehicle routing problem (VRP). It has been proven that the traveling salesman problem is a typical NP-hard and the multiple traveling salesman problem (MTSP) is the extension of the traveling salesman problem, which is more in line with the model corresponding to the actual optimization problem, so it has high theoretical research and application value.

With the help of MATLAB, this paper first applies the standard genetic algorithm (SGA) and simulated annealing algorithm (SA) to solve the multiple traveling salesman problem. Then the simulation results of the two algorithms are compared and analyzed. The results have important guiding significance for optimizing the multiple traveling salesman problem.

Based on the results of the above algorithms, the paper mainly studies the improved single parent genetic algorithm (IPGA) and multi-chromosome genetic algorithm (MCGA) to solve the multiple traveling salesman problem. IPGA adopts the idea of single parent genetics, which can’t use the crossover operation between parents. The coding method uses two-part chromosome expression. The selection operation uses the group elite selection strategy. And four mutation strategies are proposed in a targeted manner. The mutation operation uses the selective combination of four mutation strategies to eliminate the mutation probability. MCGA uses multi-chromosome encoding approach.

In the process of MATLAB experiment, the simulations are compared with the programs implemented by SGA, IPGA, MCGA and SA. The results show that IPGA and MCGA can effectively solve the multiple traveling salesman problem for the same multiple traveling salesman problem model. MCGA has reliable approximate solutions but the operational efficiency of IPGA is higher.

Key Words：Multiple Traveling Salesman Problem; genetic algorithm; simulated annealing algorithm; single parent genetic algorithms

目 录

第1章 绪论 1

1.1 研究背景与意义 1

1.1.1 研究背景 1

1.1.2 研究意义 1

1.2 国内外研究现状 2

1.2.1 智能算法研究现状 2

1.2.2 多旅行商问题研究现状 3

1.3 研究内容与预期目标 3

1.3.1 研究内容 3

1.3.2 预期目标 4

1.4 本文组织结构 4

第2章 基于SGA和SA的MTSP算法 5

2.1 相关智能算法概述 5

2.1.1 遗传算法 5

2.1.2 模拟退火算法 5

2.2 MTSP问题数学模型 6

2.2.1 最小化总距离模型 6

2.2.2 任务均衡模型 7

2.2.3 限容量模型 8

2.3 SGA求解MTSP 9

2.4 SA求解MTSP 12

2.4.1 算法流程 12

2.4.2 模拟退火算法实现 12

2.5 本章小结 13

第3章 基于IPGA、MCGA的MTSP算法 14

3.1 IPGA求解MTSP 14

3.1.1 算法流程 14

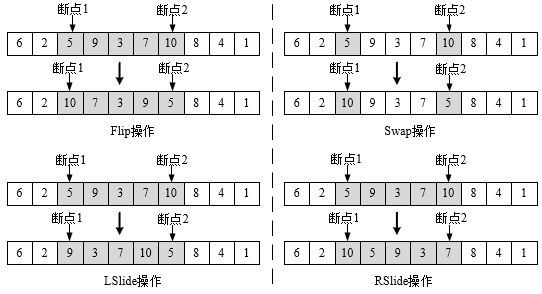
3.1.2 IPGA的遗传操作 15

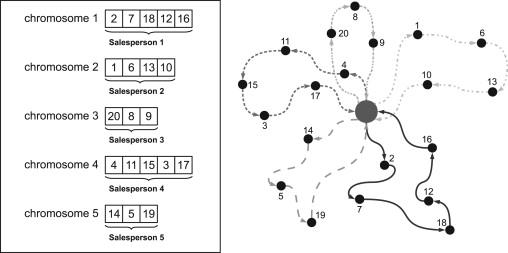
3.2 MCGA求解MTSP 17

3.3 本章小结 19

第4章 算法仿真结果及分析 20

4.1 TSP有效性测试 20

4.2 算法性能对比测试 21

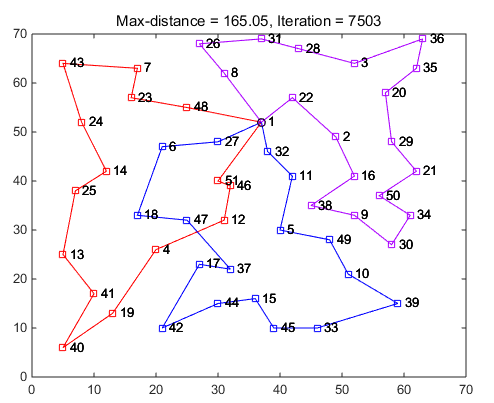
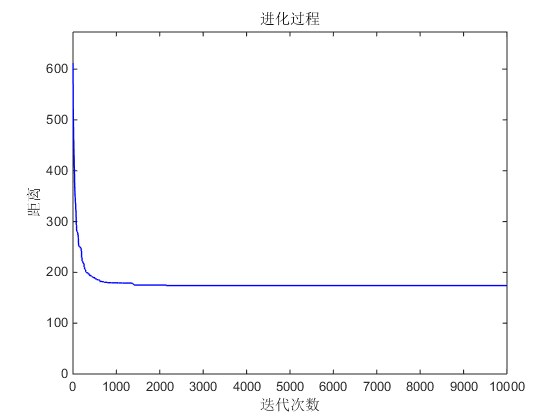
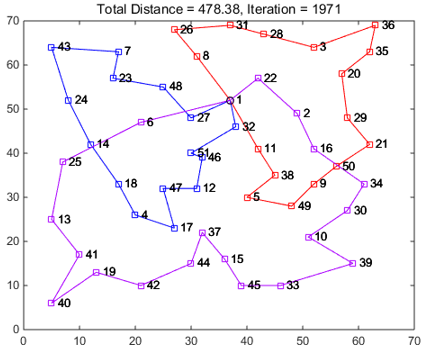
4.2.1 最小化总距离模型（Minsum）测试 22

4.2.2 任务均衡模型（Maxmin）测试 24

4.2.3 限容量模型（LCMTSP）测试 27

4.3 本章小结 29

第5章 总结与展望 30

参考文献 31

致 谢 34

第1章 绪论

解决NP问题是当代最重大的难题之一，将来或许会有人一举攻破NP完全问题，给出惊天动地的答案。直面多旅行商问题，现在要做的就是循序渐进，各个击破，不断优化智能算法，求解更复杂的模型，更难解决的情形。

1.1 研究背景与意义

1.1.1 研究背景

旅行商问题（Traveling Salesman Problem，TSP）是算法工程（algorithm engineering）的代表问题，这门研究学科重视实用性^[1]。TSP是典型的NP完全问题，到目前为止还未找到一个多项式时间的有效算法。TSP问题可描述为寻找一条最短的遍历n个城市的路径。

多旅行商问题（Multiple Traveling Salesman Problem, MTSP）是经典旅行商问题（TSP）的延伸，并且更加复杂。MTSP问题无法在多项式时间内获得最优解，因此，在大多数情况下，寻求近似解作为替代。

目前对多旅行商问题的目标评价标准主要有所有旅行商路程总和最小、所有旅行商路径的最大值最小（工作量平衡）、有容量限制（每个旅行商访问的城市个数有上下限）的所有旅行商路程总和最小。如果两个城市之间的代价在两个方向上是一致的，称为对称MTSP，反之称为非对称MTSP^[2]。本文针对所有旅行商从同一起点出发并返回起点的多旅行商问题，例如快递公司送货，本文考虑了上述三种评价标准，并用所提智能算法来分别求解，实验结果表明改进单亲遗传算法（IPGA）和多染色体遗传算法（MCGA）能较好地求解MTSP问题。为了更全面的了解多旅行商问题，本文还考虑了m个旅行商从不同起点出发并回到各自起点的多旅行商问题，例如多仓库物流配送问题和全国连锁店的送货问题，通过对其进行MATLAB仿真实验，验证了本文所用算法的有效性。

1.1.2 研究意义

多旅行商问题比经典TSP问题更复杂，求解也更为困难，MTSP的应用更加广泛，也更加符合现实问题，如快递员送货、车辆的路径规划、应急物资配送^[3]、多无人机协同侦察路径优化等。

容量限制的多旅行商问题和任务均衡的多旅行商问题是TSP和MTSP问题的扩展模型，其给每个旅行商安排一个合理的访问城市个数作为约束条件或使每个旅行商的工作量平衡，这样更符合实际应用领域，同时合理的分配旅行商工作任务，能够提高工作效率，因而具有较高的理论研究和应用价值。

与TSP相比，尽管MTSP具有更高的求解难度，但它具有更广泛的应用，特别是在各种路由和调度问题中。根据起点的数量，MTSP可分为四种形式：单起点开环、单起点闭环、多起点开环、多起点闭环。这些情形均可以对应不同的场景和不同的实际应用。例如，当MTSP只有一个起点时，它更适合快递服务。另一方面，当MTSP包括多个起点时，这是对现实情况更充分地模拟，它可以用于许多问题，例如热轧调度^[4]，车辆调度问题等等。此外，如果MTSP的任务考虑时间窗限制，MTSP可以被视为具有时间窗的多旅行商问题（MTSPTW）。MTSPTW应用于任务规划问题和某些货物运输情况，例如码头集装箱的运输调度问题。简而言之，研究MTSP及其变化是非常重要和有价值的。

目前不同智能算法之间的结合应用是研究的热点，例如将模拟退火算法与遗传算法相结合用于求解模糊聚类问题，算法之间互相取长补短，使该组合算法更有效、更快速地收敛到全局较优解。虽然SAGA已经被广泛应用，失去了新颖性，但是这种用不同算法互相结合的思想来克服单一算法的局限性是很值得去深究的，甚至不止两种算法相互结合。在MTSP领域，如果有人提出了新的算法思想并成功解决难题或者已知算法得到了较好的优化，消息会很快传播开来，应用于更多领域。

1.2 国内外研究现状

1.2.1 智能算法研究现状

智能算法是一门边缘交叉学科，是生物、数学、物理等多学科的完美融合，大都是20世纪60年代末开始流行起来的，起初是人们对大自然界演化现象的简单模仿而来的，其要解决的一般是最优化问题。近年来，随着计算机技术的飞速发展，一系列新的仿生智能算法应运而生，且它们之间呈现出相互结合优化改进的趋势。智能算法能较好地解决大规模复杂系统中出现的组合优化问题，运用领域十分广泛。Yang Jian和Yang Li采用蚁群算法来提高智能机器人的视觉认知功能^[5]。T. P. Latchoumi等人尝试通过粒子群算法（PSO）解决与空化水喷丸相关的水射流加工问题^[6]。YuCun Zhang等人将人工免疫算法应用于典型环锻的几何参数测量，可以确保模型的尺寸参数的精度^[7]。K. Prakash Kumar等人采用人工鱼群算法来解决微电网中可再生能源产生的能量的最优调度问题^[8]。Wenhua Han等人采用狼群算法来实现智能电网精确时间同步控制，狼群算法主要用来自动调整PID控制器的最优参数^[9]。B. K. Patle等人介绍了萤火虫算法（FA）在不确定环境下移动机器人导航的应用和实现^[10]。Yongquan Zhou等人采用改进的猴群算法来解决0-1背包问题^[11]。Tao Meng和Quan-Ke Pan提出了一种改进的果蝇优化算法求解多维背包问题^[12]。在人工智能研究领域，智能算法是其重要的一个分支。目前智能计算正在蓬勃发展，研究人工智能的领域十分活跃，人们在不断地探索新理论、新方法和新技术，未来这些研究成果将给人类世界带来巨大的改变^[13]。

1.2.2 多旅行商问题研究现状

在多旅行商问题中，一个任务由多位旅行商共同完成，其问题的求解难度较经典旅行商问题更大，用于经典旅行商问题求解的方法或策略不能简单地应用于多旅行商问题的求解，有关该问题的研究成果远比经典旅行商问题少^[2]。

对多旅行商问题的研究是从20世纪七十年代开始，最初主要采用精确算法来求解，例如线性规划方法、动态规划方法、分支定界方法等，但随着问题规模的扩大，精确算法很难有效地求解MTSP问题，后续的研究工作逐渐倾向于采用启发式算法或元启发式算法^[2]。大多数研究方法都是先将MTSP转化为TSP，然后在转化得到的TSP基础上利用现有TSP的求解算法进行求解。

目前有很多学者提出了更加复杂的MTSP模型，并联系具体的实际问题进行了仿真实验。J. Li等人提出了一个名为CTSP的新MTSP，其中不同的旅行商拥有独家城市集并共享一组共同的城市，其中每个独家城市集具有特定旅行商可访问的独特颜色，而共享城市具有多种颜色，只允许具有相同颜色的旅行商访问^[14]。Xinye Chen等人提出了一种基于蚁群算法的模因算法，可同时优化MTSP的总行程距离和最大行程长度，提出的算法适用于多起点多旅行商问题（MD-MTSP）和单起点多旅行商问题（SD-MTSP）^[15]。Yongbo Chen等人针对多旅行商问题提出了改进的两部分狼群搜索算法（MTWPS）^[16]。Shuai Yuan等人提出了一种新的交叉算子，称为两部分染色体交叉（TCX），用在遗传算法（GA）中求解多个旅行商问题^[17]。Pandiri Venkatesh和Alok Singh 提出了MTSP的两种元启发式方法，第一种基于人工蜂群算法，第二种基于入侵杂草优化算法，他们还加入了局部搜索算法来进行改进^[18]。王勇臻等人提出了求解多旅行商问题的改进分组遗传算法^[19]。

1.3 研究内容与预期目标

1.3.1 研究内容

本文借鉴常用遗传算法和模拟退火算法求解旅行商问题的思想，使用这两种算法来求解不同目标函数评价标准的MTSP模型，主要研究工作包括：

（1）在阅读大量有关智能算法与旅行商问题书籍的基础上，深刻理解多旅行商问题的智能算法求解思想，学习借鉴近年来与求解MTSP问题相关的参考文献，在这个过程当中对比各篇文献求解的思想与方法，总结其优势与不足；

（2）通过深入分析遗传算法和模拟退火算法在多旅行商问题中的实际应用模型，分别掌握求解MTSP问题的具体流程，并针对本文所提出的三种多旅行商问题的目标函数评价标准和两种多旅行商问题模型，分别用常规遗传算法、改进单亲遗传算法、多染色体遗传算法和模拟退火算法来对这些问题进行求解；

（3）借助MATLAB数学软件编程，在Intel（R）Core（TM）i3-5005U CPU@2.00GHz计算机环境中对所提MTSP问题的四种智能算法运行测试，用TSPLIB中的常用数据集进行实验，对所得实验结果进行综合比较分析，得出实验结果与结论。

1.3.2 预期目标

通过理解和掌握常规的标准遗传算法和模拟退火算法求解MTSP问题的原理和步骤出发，运用MATLAB软件编程来实现多旅行商问题的设计与仿真，通过对这两种算法的仿真结果进行比较分析，找出各算法存在的局限和优势，然后对标准遗传算法进行改进，根据具体问题的具体情况设计遗传编码方式和进化策略，使该算法更有效、更快地收敛到全局较优解，争取达到目前已知的全局最优解。

1.4 本文组织结构

第1章 介绍了课题研究的背景、目的及意义，对国内外研究现状、研究内容、预期目标等进行了综合论述。

第2章 介绍了标准遗传算法（SGA）和模拟退火算法（SA）的理论基础，包括算法原理、特点和具体应用领域，此外还描述了不同MTSP的数学模型和用SGA和SA来求解MTSP的实现过程。

第3章 描述了改进单亲遗传算法（IPGA）和多染色体遗传算法（MCGA）的MTSP算法的具体实现过程。

第4章 对本文所提出的算法进行了MATLAB仿真实验，并针对不同的MTSP模型分别进行仿真结果分析。

第5章 总结了本文的工作内容，明确了所用算法的有效性和局限性，并对今后的研究方向进行了展望。

第2章 基于SGA和SA的MTSP算法

2.1 相关智能算法概述

2.1.1 遗传算法

遗传算法（Genetic Algorithm，GA）是由美国Michigan大学Holland教授首先提出来的，是模拟达尔文生物进化论中“物竞天择、优胜劣汰”的演化法则，并结合遗传学机理的一种优化算法，简单来说就是通过模拟生物进化过程寻找最优解。遗传算法是用于解决最优化问题的一种智能算法，是进化算法中的一种^[13]。

遗传算法是把问题参数编码组成初始种群后，通过模拟生物基因遗传操作来实现优胜劣汰的进化过程，最终生成符合优化目标的解^[20]。

遗传算法具有以下几方面的特点：

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：