摘 要

在复杂网络中，对网络节点的中心性（或称影响力、重要性）的评估一直以来都是一个重要的研究主题。节点的影响力直接决定了网络的性质和特点，在搜索引擎、社交网络、电力系统、生物生态系统等诸多领域有着重要的应用。本文首先对度中心性（Degree centrality）、介数中心性（Betweenness centrality）、Pagerank等方法进行了回顾和分析，接着信息熵/信息维度模型和k-medoid聚类模型进行了深入的分析，并基于这两种方法的基础上提出了一种k-path optimization算法，该算法相较于之前的方法，显著降低了计算复杂度，并且在小世界网络上效果十分突出。

论文主要研究了对于信息熵/信息维度模型进行简化的可能性、与k-medoid方法相似的优化方法的可行性，进而对所提出的算法进行优化、测试，并与其它方法进行对比。此外，本文还提出了一种基于雷达图的多维度节点影响力评估方法，改变了由单一中心性指标进行评价的传统方式。

研究结果表明：k-path optimization算法相较于之前的方法，显著降低了计算复杂度，并且在小世界网络上效果十分突出。

本文的特色：提出了k-path optimization算法、提出了基于雷达图的多维度节点影响力评估方法。

关键词：机器学习；复杂网络；节点影响力；小世界网络；传播影响力

Abstract

In complex networks, the assessment of the centrality of nodes has always been a fundamental issue. The influence of the node directly determines the nature and characteristics of the network, and has important applications in many fields such as search engines, social networks, power systems, and biological ecosystems. In this paper, the methods Degree centrality, Betweenness centrality and Pagerank are reviewed and analyzed. Then the information entropy/information dimension model and k-medoid clustering model are deeply analyzed. Based on these two methods, a k-path optimization algorithm is proposed. Compared with previous methods, the algorithm in this paper significantly reduces the computational complexity and is very effective on Small-world Networks.

The paper mainly studies the information entropy/information dimension model and the feasibility of the optimization method similar to the k-medoid method. Then the proposed algorithm is optimized, tested and compared with other methods. In addition, this paper also proposes a multi-dimensional node influence evaluation method based on radar chart, which changes the traditional way of evaluation by a single centrality.

The research results show that the k-path optimization algorithm significantly reduces the computational complexity compared with the previous method, and the effect is very prominent on the small world network.

The characteristics of this paper: The k-path optimization algorithm is proposed, and the multi-dimensional node influence evaluation method based on radar chart is proposed.

Key Words：Machine Learning；Complex Network；Node Influence；Small-world Network；Communication Influence

目 录

第1章 绪 论 1

1.1 研究背景 1

1.2 国内外研究现状 1

1.2.1 复杂网络节点 1

1.2.2 机器学习 2

1.3 本文研究工作与内容安排 3

第2章 基于结构的中心性指标评价方法 4

2.1 度中心性 4

2.2 介数中心性 4

2.3 Pagerank 7

2.4 紧密度中心性 8

2.5 本地中心性 9

2.6 本章小结 10

第3章 基于传播的中心性指标及相关分析 11

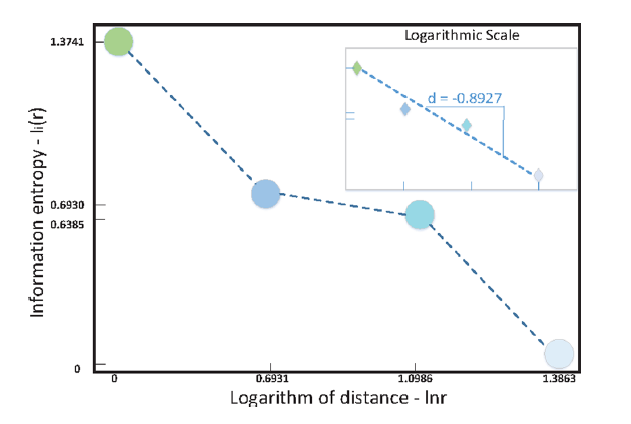
3.1信息维度 11

3.1.1局部维度Local dimension 11

3.1.2信息熵 11

3.1.3节点信息维度 12

3.2聚类分析 13

3.2.1信息传递概率矩阵 13

3.2.2聚类算法k-medoid方法 14

3.3小世界网络 15

3.4本章小结 16

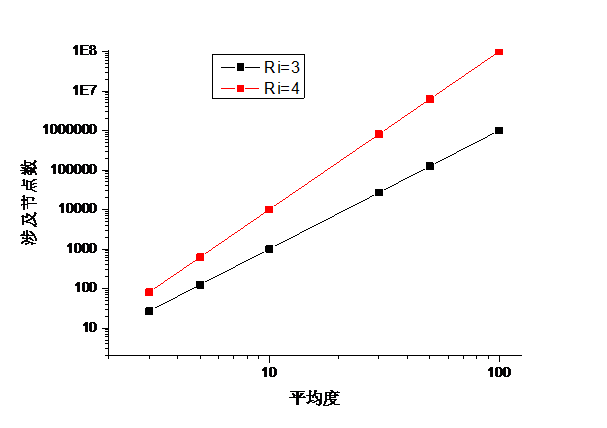
第4章 k-path optimization方法 17

4.1最大值迭代算法（k-path optimization） 17

4.2测试 20

4.2.1算法效果 20

4.2.2时间复杂度 22

4.2.3空间复杂度 22

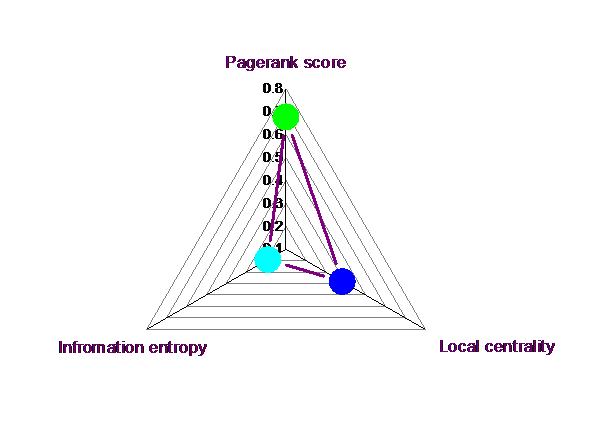
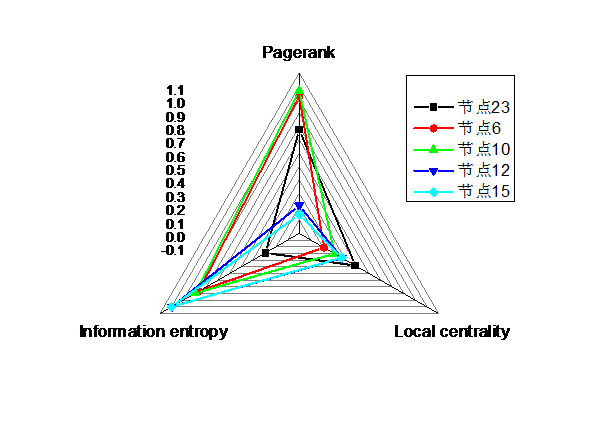
4.3基于雷达图的多维度影响力分析 23

4.4本章小结 24

第5章 总结与讨论 25

5.1结论 25

5.2展望 25

参考文献 26

致谢 31

第1章 绪 论

1.1 研究背景

自然界和人类社会中广泛存在着复杂系统，而复杂网络是描述这些系统的重要手段。而且在现实世界中，诸多复杂系统以网络形式呈现。因此，复杂网络已经成为当今复杂系统或复杂性科学研究中最受关注和最具挑战性的科学前沿课题之一^[1]。生物系统中的蛋白质相互作用网、基因调控网、病毒传播网络，科技系统中的互联网、电力系统^[2]，社会系统中的社交平台^[3,4]、电子邮件网、通信网、交通网等，都是典型的复杂网络。这些网络由节点和边构成，其中节点代表实体，边代表实体间的关联^[5]。近年来，节点重要性排序研究受到越来越广泛的关注，不仅因为其重大的理论研究意义，更因为其广泛的实际应用价值^[6]。此外，对于节点重要性的排序研究有利于设计网络，使人工的复杂网络(如电网、通讯基础设施等)能够具有更强的性能和鲁棒性。例如文献^[7]中的工作就通过对节点影响力的分析优化设计有效的传播策略。

一个成熟的排序算法一般要包括如下特性^[8]：中心化指标应该是对称的，如果对网络的节点重新编号，中心化指标应该不变；无论将一个节点看成整个图的节点，还是将其看成一个连通分支的节点，所得到的中心化指标的值应该一致；孤立节点的中心化指标应该最小；在具有链式结构的网络中，节点的中心化指标应该从边缘向中心递增，即越靠近中心，节点的中心化程度应该越高；在所有的具有n个节点的连通网络中，链式结构网络的顶端节点的中心化指标应该最小，而星型结构网络的中心节点的中心化指标应该最大；移去某个节点的某条边，至少不会增加该节点的中心化指标。

1.2 国内外研究现状

1.2.1 复杂网络节点

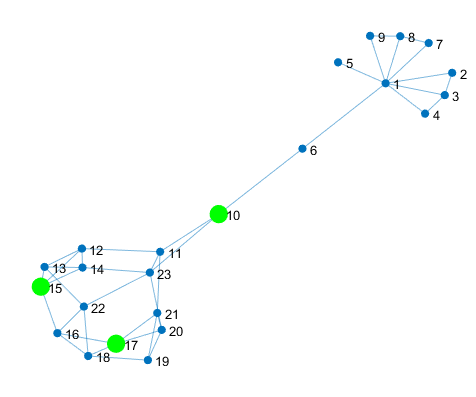
在学术界对网络节点影响力分析算法的不断研究中，许多重要的方法被提出。其中最早且最基本的就是度中心性^[9]，度中心性(Degree Centrality，Centrality直译为中心性，一些文献中亦称指标，下文均以中心性相称)是研究无标度网络拓扑结构的基本参数，用于描述在静态网络中节点所产生的直接影响力，其值为与该节点直接相连的节点数。文献^[10]对度分布指数与其拓扑结构、形成原因及传播动力学之间的关系进行了系统的研究。在度分布指数的基础上，紧密度中心性(Closeness Centrality，又称接近中心性) ^[11]、特征向量中心性(eigenvector centrality) ^[9]、介数中心性(Betweenness Centrality)、k-壳分解法(k-shell decomposition) ^[12]、半局部中心性^[13]、流介数中心性(flow betweenness centrality) ^[14]、累计提名(cumulative nomination)算法^[15]、节点收缩法^[16]、H-度中心性^[17]等。其中最值得说明的是，H-度中心性是一种含权的排序方法，它考虑了网络中每个链接性质和能力的不同。类似的研究见于^[18]。详细的总结可见于2014年的文献^[19]。但是这些指标各有优缺点，很多指标在一些方面的性能很好，但却不可避免的牺牲了一些其他方面的性能。为解决此问题，研究者基于多属性决策原理提出了多属性模型^[20]，类似的研究还可见于^[21,22]。文献^[23]将半局部中心性扩展到加权复杂网络，文献^[24]在k-shell分解法的基础上提出了核心中心性，文献^[25]进一步提出了一种基于k-shell分解法迭代因子的评估方法，文献^[26]在各种中心性方法的基础上研究了节点的扩散能力，文献^[27]基于Dempster-Shafer理论提出了新的中心指标方法，文献^[28]将识别最有影响力节点的问题映射到随机网络中的最佳渗透理论，取得了重要的进展。很多网络具有社团结构，传统的排序算法在社区结构下有一定的局限性，因此Zhang等人^[29]提出了一种基于k-medoid算法的重要节点定位方法，这也是机器学习方法在该主题下很重要的一个应用，因此在这个视角下的节点影响力也具有研究价值，相关文献见于^[30,31]。

1.2.2 机器学习

近年，机器学习(Machine Learning)开始用于复杂网络的节点分析，但相关工作仍然非常少。一个例子是在^[32]中，作者提出了node2vec算法框架以学习网络中节点的连续特征表示，而在^[33]中，作者通过Net-Net自动机器学习来实现计算预测，以克服大规模复杂网络难以确认所有节点和链接的问题。

机器学习是近年的研究热点^[34]。由于该领域的繁荣，我们很难在较短的篇幅中概括机器学习各个发展方向。针对复杂网络节点影响力分析与设计，机器学习有望提供一个较之传统方法更准确且更具有普适性的方法。图形神经网络(GNN)近年来越来越受欢迎^[35]，是一个很有潜力的方向。自动机器学习(AutoML)^[36,37]旨在将机器学习中的重要步骤自动化，如功能，建模，优化和评估。多标签学习是一个重要的发展方向^[38]。一些研究人员^[39]通过寻找帕累托最优解的目的，将多任务学习作为多目标优化。

此外，在本文中，有必要花费专门的一章篇幅简要总结一下这种正处于爆发期的机器学习方法--深度学习(Deep Learning)。近年来，深度学习取得了巨大的成功。作为机器学习的一个引人注目的研究点，深度学习逐渐成为数字信号处理的重要技术，主要可以分为多层感知器( multilayer perception，MLP)^[40]，卷积神经网络( convolutional neural network，CNN)^[41]，循环神经网络( recurrent neural networks，RNN)^[42]。有关深度学习及其近期历史的介绍，请参阅^[43]。最新的发展还包括长短时记忆网络( long short-term memory，LSTM)，生成式对抗神经网络(Generative Adversarial Networks，GANs) ^[44]。在基础深度学习领域，批量标准化（BatchNorm）作为一种广泛采用的技术引起了极大的关注^[45]，这种技术可以实现更快，更稳定的训练。 CNN近年来取得了巨大的成功，特别是在计算机视觉领域，但研究人员仍在推进研究前沿，有学者提出了加权信道丢失（WCD）^[46]以降低CNN的计算成本。 ^[47] 提出了DIFFPOOL，可以以端到端的方式与各种GNN架构相结合。值得注意的进展还包括周志华等人提出的深度深林^[48]。

1.3 本文研究工作与内容安排

本文首先介绍识别复杂网络中各个重要节点的方法，然后将会介绍信息维度方法、聚类方法、传播模型和小世界网络，最后在此基础上介绍了本人设计的基于机器学习的复杂网络节点影响力分析方法和基于该方法之上的一种新的网络节点重要性评估模型：k-path optimization。本课题将会考虑在小世界网络上进行快速的中心节点定位，这种方法很容易应用在实际的网络上，具有很好的研究前景。

本文的主要内容如下：

第一章 对复杂网络的诞生历史、国内外复杂网络节点分析的主流研发和发展趋势做归纳总结，从而引出本文的创新之处和算法设计方法。

第二章 简单地对几种经典的复杂网络节点影响力分析理论进行介绍，并分析了它们的性能。

第三章 介绍了作为本文基础的几项研究成果，包括k-medoid聚类分析、渗透理论、信息熵理论等，还介绍了小世界网络的基本概念。

第四章 介绍如何基于Matlab，测试算法的性能，并将其运用在较大的网络上。并计算其复杂度。

第五章 将对本课题所完成的工作及其达成的目标进行总结分析，并对不足点进行补充，提出未来工作的展望。

总体而言，通过机器学习方法，基于信息熵模型，本文设计了一种复杂网络中心节点的定位算法。

第2章 基于结构的中心性指标评价方法

2.1 度中心性

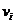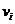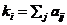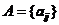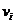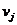记一个无向简单网络为G（V，E），其中V和E分别是节点集和链路集，节点的度，表示为，定义为与的直接相连的邻居的数量。数学上，，其中是邻接矩阵，即如果和连接则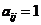，否则为0。度中心性（Degree Centrality）是识别节点影响的最简单的指标：节点拥有的连接越多，节点的影响就越大。

为了比较不同网络中节点的影响，将归一化度中心性定义为

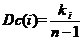（2.1）

其中n = |V|是G中节点的数量，n-1是最大可能度。需要注意的是，上述归一化实际上只是为了方便，也就是说，即使使用归一化度中心性，不同网络中的节点通常也不具有可比性，因为这些网络的组织，功能和密度是不同的。

度中心性的简单性和低计算复杂性使其具有广泛的应用。有时度中心性表现出色，例如在网络脆弱性的研究中，与基于更复杂的中心性模型的一些方法（如介数中心性，紧密度中心性和特征向量中心性）相比，针对度的攻击可以非常有效地破坏无标度网络和指数网络^[49]。此外，当扩散速率非常小时，度中心性相较于特征向量中心性和其他一些众所周知的中心性指标^[50,51]而言，是识别节点扩散影响的一个更好的指标。

在有向网络D（V，E）中，每个链路都与一个方向相关联，然后我们应该分别考虑一个节点的出度和入度。例如在社交网络中，如果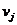是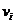的前驱节点，则从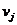节点到节点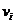存在有向链接，那么节点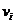的入度（即具有指向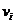的有向链接的节点的数量）反映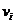的受欢迎程度，而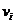的出度（即从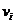到其他节点的链接数量）在某种程度上代表了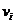的社交活动[54]。在加权网络中，度中心性通常由权重代替，权重定义为相关链接的权重之和。

2.2 介数中心性

介数中心性（Betweenness Centrality）以节点控制网络中信息流的潜在能力为视角。这种模型首先由Bavelas于1948年提出^[52]，1977年，Freeman ^[53]概括了中心性的图论理论概念，并将其扩展到连接和非连接网络，显示了我们今天使用的方式。一般来说，存在从节点开始并以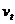结束的多于一条的最短路径，可以通过计算通过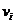的所有最短路径来计算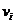的信息流的可控性。因此，节点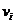的介数中心性可以定义为

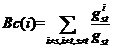（2.2）

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：