英语原文共 6 页，剩余内容已隐藏，支付完成后下载完整资料

---

毕业论文（设计）

英文翻译

原文标题A Sliding Mode Control Approach to Longitudinal Control of Vehicles in a Platoon

译文标题 队列中车辆纵向控制的滑模控制方法

队列中车辆纵向控制的滑模控制方法

Yunlong Ying Tao Mei, Yan Song, Yue Liu

1 中国科学技术大学自动化系，中国 安徽 合肥

2 中国科学院先进制造技术研究所，中国 安徽 合肥

摘要：在实际驾驶条件下，如平坦的弯道或复杂的道路交通条件下，队列的速度往往在加速或减速上发生变化，这将造成间距误差明显增大，甚至造成队列系统不稳定。因此，本文提出了一种鲁棒控制技术来解决这一问题。本文所采用的鲁棒控制策略是滑模控制(SMC)，对系统参数变化和外部扰动具有很强的鲁棒性。本文设计了两个控制器来控制队列中内车辆的速度和方向。采用滑模控制技术对纵向控制器进行控制，以在期望的间隔范围内调节车辆之间的纵向距离。横向控制通过转向控制器对齐车辆方向，而转向控制器实际上是PID控制器。实验仿真结果表明，所设计的模型可以实现车辆跟踪控制的稳定性。所设计的两个控制器可以保证车辆保持在参考路径上，且车队的间距误差和横向误差相对较小。

关键词：车辆模型，队列控制，滑模控制，纵向控制器，转向控制器

1. 引言

最新统计显示，中国每年约有10万人死于交通事故，其中92%是人为因素造成的，此外，交通堵塞主要是由交通违规引起的。因此，许多与驾驶相关的技术通常都是为了减少操作错误的影响和基本驾驶程序职责的不足而设计的。减少交通事故数量和优化利用高速公路通行能力的一个机会是自主车队的概念（车辆群跟随领头车辆，车辆以较小间距行驶）。车队的移动与传统的系统相比有许多优点。首先，自动驾驶可以提高驾驶的准确性和稳定性，减少因人工驾驶而引起的交通事故。其次，在车队内的车辆之间的可以实现较小的距离行驶，从而增加了最大的道路通行能力。此外，这还有助于优化交通流，减少空气阻力所带来的油耗。

在自动驾驶车队的课题中，对自动驾驶车队的可行性和稳定性进行了评价和论证。在Konvoi项目中，四辆试验车配备了所需的汽车技术来构建卡车车队，在队列内，车辆之间可以实现以比较近的距离行驶。卡车耦合保持一个很短的间隔（大约10米）在高速公路上组成卡车车队[1-4]。介绍了从意大利到中国的一次带着四辆电动自动驾驶汽车的旅行，重点讨论了挑战的各个方面，从管理问题到最技术性的问题[5-8]。车辆跟踪应用是系统测试连续三个月和13000公里长的独特经验。虽然总结了许多主要的自动驾驶车辆项目，但它们都寻求通过开发技术来提高道路的安全性和效率，使车辆能够在没有人工驾驶的情况下运行[9]，很少有人讨论自动驾驶汽车大规模实施时的性能问题。然而，到目前为止，对于车辆速度随道路曲率的变化对间距的影响的讨论还很少。在本文中，我们可以看到间隔误差随着速度的急剧变化，由于控制律的复杂度低，沿队列的间距误差增大，甚至导致自动驾驶车队的不稳定。

间隔波动的另一个重要原因是通信时延和高频噪声。Shladover提出了一个制导模型[10]，在该模型中，头车的速度和加速度信息被传送给所有跟驶车辆。该模型具有通信信道扰动或时延[11]。所以No等人建议在车辆和跟随车辆之间进行局部通信[12]。CC Chien提出了一种基于前车和跟随车前后信息的车辆队列控制算法[13]。这些模型或多或少都存在通信信道干扰或时延。为了解决这种通信干扰问题，提出了一种新的车辆排系统控制模型。本文提出了一种不需要全局通信和本地通信链路的信息需求较少的方法。用于实现队列控制的信息由各种机载传感器收集。采用滑模控制技术可以解决速度波动和噪声问题。本文采用滑模控制算法[14-18]设计了纵向控制器。滑模控制方法的选择主要取决于保证一定的鲁棒性和抗扰动的必要性，并且参数的变化影响了车辆的模型，并受到控制律的低复杂度的影响。

本文的结构如下。第二节介绍了在仿真模型中使用的车辆运动方程。第三节详细描述了队列系统及其仿真模型。第四节阐述了基于滑模控制的纵向控制方案。第五节给出了实验结果，最后在第六节对实验结果进行了总结。

1. 车辆模型

本文假定排内所有车辆都是相同的，可以采用著名的自行车模型来给出其纵向和横向动力学的充分准确的表示。对于车辆模型，我们可以用下列微分方程组来表示我们的车辆系统[14]。第一代车辆的模型如下：

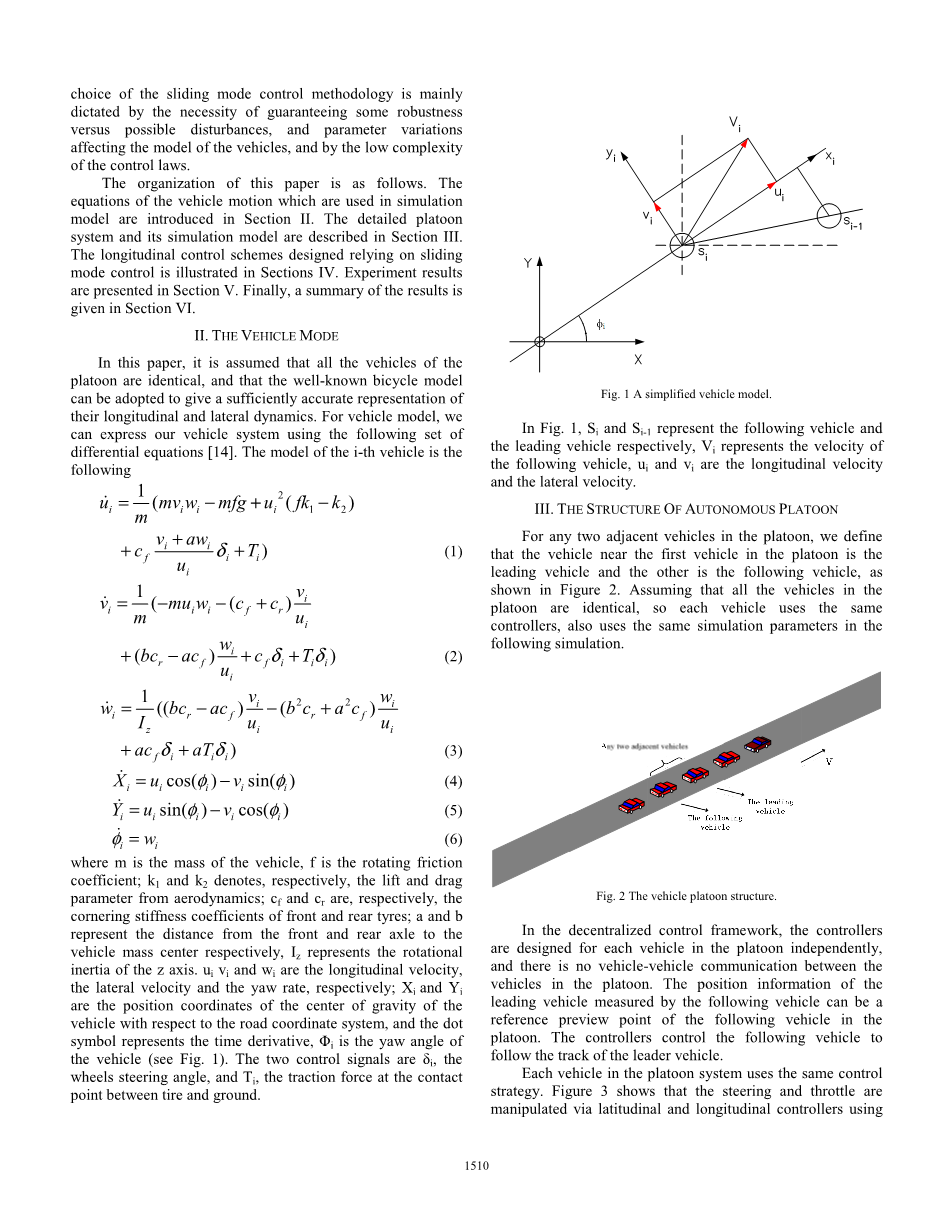
其中m是车辆的数量，f是旋转摩擦系数；和分别表示空气动力学中的升力和阻力参数；和分别表示前、后轮胎侧偏刚度系数；a和b分别表示从前轴和后轴到车辆质量中心的距离，代表z的转动惯量。轴心。和分别表示车辆的纵向速度、横向速度和偏航速率；和是车辆重心相对于道路坐标系的位置坐标，点符号代表时间导数；ĭi是车辆的偏航角(见图1)。两个控制信号是：表示车轮转向角，表示轮胎与地面接触点处的牵引力。

图1 简化车辆模型

在图1中，和分别表示以下车辆和领先车辆，代表以下车辆的速度，和表示纵向速度。

1. 自动驾驶车队的结构

对于队列中的任意两个相邻车辆，我们定义队列中第一个车辆是领先车辆，其他的是跟随车辆，如图2所示。假设队列中的所有车辆是相同的，所以每个车辆使用相同的控制器，在下面的仿真中也使用相同的仿真参数。

图2 车辆队列结构

在分散控制框架下，控制器是独立为队列内的每辆车设计的，没有车队车辆与另一车队车辆之间的通信。由以下车辆测量的前车位置信息可作为排中以下车辆的参考预览点。控制器控制以下车辆以跟踪领头车辆的轨迹。

车队系统中的每一辆车使用相同的控制策略。图3显示，转向和节流阀是使用来自参考路径、车辆状态和传感器信息的输入，通过横向和纵向控制器操纵的。在所提出的队列模型中没有汽车、道路和车辆之间的通信，所有所需的状态信息都是由车载传感器获得的。根据不同的状态信息，控制算法计算出两种控制器所需的间隔误差和横向误差。间距误差是纵向控制器的输入，纵向控制器的输出是车辆模型中用来改变车辆纵向速度的牵引力。纵向控制器确保保持领先车辆和后续车辆之间的时间或空间间隔。横向误差是转向控制器的输入，转向控制器输出所需的车轮转向角，用于控制车辆的方向。转向控制器确保车辆相对于期望路径的横向偏差最小化。在两个控制器的协同作用下，队列在参考路径上保持一定的间隔。

为了确保乘客有合法舒适和安全的体验，我们在控制器的输出中增加了一些限制，限制了正常路径下的制动/节气门和正常路径跟踪操作下的转向操作。当输出信号超出极限范围时，仿真停止。由于物理和舒适的原因，这两个输出信号是饱和的。

图3 以头车的信息为输入，车辆模型、纵向和转向控制器为子系统的框图

1. SMC控制器设计

在设计滑模控制器之前，首先考察了采用传统PID控制器作为纵向控制器时，间距误差的变化。为了评估本文提出的模型和控制器，采用了由两条直线和一条曲线组成的三段路径，如图4所示。

在图5中，您可以发现，当具有道路曲率的车辆的速度发生相应的加减速变化时，间距误差会显著增加，特别是在道路弯曲较大的路段，如急转弯，车队系统可能会变得不稳定，当使用传统的PID控制器时，跟随车辆将无法正常地跟随先导车辆。因此，我们必须设法消除或减少由于车辆速度随道路曲率的变化而引起的间距误差的增加。

图4 使用纵向和转向控制器跟踪多段路径的四辆车辆

图5 当队列以变化的速度移动时，期望相邻车辆之间距离为10米的PID控制器的间距

采用滑模变结构技术设计车辆纵向控制器可以解决上述问题。第i辆车纵向控制的目的是保持与前一辆车辆所需的安全距离，其中i=1，2，hellip;，n。为了使实际相对距离等于所期望的安全距离，车辆选择的滑动变量是所需间距与实际间距之间的误差，即

其中是第i-1辆车与第i辆车之间的实际纵向距离。参数可由安装在车辆前部的激光传感器测量。

在这种情况下，控制任务是设计一个能够使滑动变量在有限时间内消失的控制律。

通过滑模设计方法，将开关函数定义为

其中和是设计参数。控制律可以选择为

其中是一个考虑到物理和乘客舒适极限的正设计参数。

本文利用切换函数(8)定义Lyapunov函数如下

如果我们对上述李亚普诺夫函数进行微分，我们只需得到

从(9)，我们得到

因此，可以在有限的时间内进入滑模面，直到达到平衡点。

(8)的推导是

(7)的第二次导数是，

然后我们得到

从(9)和(14)，我们得到

对于我们得到

从(1)和(16)出发，给出了第i辆车牵引力的拟议控制律

证明了控制律(17)能在有限时间内保证间距误差收敛到零。

在此基础上，研究了滑模超曲面中队列间距误差动力系统的稳定性。从=0，i=1，2，hellip;，N，我们得到

然后给出了间隔误差的滑模运动方程

利用向量Lyapunov函数方法[19]，我们得到了零解的指数稳定条件

因此，当和为正值时，队列系统是串稳定的。

1. 仿真结果

为了验证所提出的控制器的性能，对四辆车组成的队列系统进行了实验仿真。这篇文章没有讨论关于使用车载传感器获取车辆前运动状态的条件，假设所有需要的信息都是由机载传感器和感知算法提供的。

为了证明所设计控制器的优越性，本文对PID控制器和滑模控制器的性能和优点进行了比较。车辆模型的参数见表1。

表1 车辆模型参数

车辆的初始位置和速度如下

头车开始在车道上移动，随着道路的弯曲而改变。假设所有想要的间距都是=10m。仿真中使用的控制参数如下：=4，=3，=1.5，=0.5rad，=16000N。队列中领头车辆的参考速度如图6所示。图4中设计的SMC控制器演示了队列中四辆车的运动轨迹；图7是图4圆圈中曲线的部分放大细节。从图7中，我们可以看到四辆车的轨迹基本是重合的，甚至在道路的弯道上也是如此，因此，后续车辆可以在较小的横向误差中稳定地跟随前车。

纵向速度的演变情况见图8。通过PID控制器和所提出的滑模控制器获得的间隔误差分别在图9和图10中得到了报告。表二给出了PID控制器与SMC控制器的间距误差比较，表明采用SMC控制器的排系统比采用PID控制器的队列系统具有更好的稳定性。图11示出了SMC控制律的横向误差的变化。图12示出队列中下列车辆的纵向力和转向数据。由于道路转弯半径很大，车辆的转向角很小。仿真结果表明，在设计的SMC控制器下，间隔误差收敛速度较快。与PID控制器相比，滑模控制器可以大大降低队列内车辆速度变化引起的间距波动，不顺着车队放大间距误差，可以保证排系统的稳定性。

图6 头车的参考速度

图7 在图4中圆的部分放大细节

表2 以下车辆PID控制器与SMC控制器间距误差的比较

图8 队列内车辆的纵向速度

图9 PID控制器的间隔误差

图10 SMC控制器的间距误差

图11 SMC控制器的横向误差

在有限的时间内，当队列中的车辆都在连续三段的参考路径上时，车辆之间的横向误差为零。

图12 队列内跟随车辆的纵向力和转向数据

1. 结论和今后的工作

本文提出了一种车辆排纵向控制器和转向控制器。采用滑模控制技术设计了纵向控制器，我们使用PID控制器作为横向控制。仿真结果表明，滑模控制律保证队列内车辆与前车保持预定距离，而且队列系统是稳定的，即队列内车间距误差不会沿队列增大。在未来，我们将通过各种车载传感器实现更多关于上述车辆的信息，并尝试在车辆运动状态的纵向力和侧向力之间的关系中考虑耦合。

感谢

本研究由国家自然科学基金91120307和91320301资助。

参考文献

[1] Kunze, R., C. Tummel, and K. Henning. 'Determination of the order of electronically coupled trucks on German motorways.' Power Electronics and Intelligent Transportation System (

剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[20511]，资料为PDF文档或Word文档，PDF文档可免费转换为Word