摘 要

本文从切换系统、正系统延伸到切换正系统，讨论系统的重要性质，即稳定性。关注具有稳定和成对可交换子系统的切换正线性系统的共同线性余正李雅普诺夫函数的存在性问题。分别考虑：仅包括连续时间子系统、仅包括离散时间子系统、混合连续时间子系统和离散时间子系统的三个系统。利用推导证明，只要线性切换正系统的子系统是连续时间，离散时间或混合类型，且符合其中任意子系统可两两交换，就可以构建共同线性余正李雅普诺夫函数，从而得出整个系统是稳定的。在证明中，首先考虑子系统数量为2的情况，然后将得到的结果利用数学归纳法发扩展到一般情况。最后利用MATLAB给出的数值例子来验证所证明结果的有效性。

关键词：切换系统；正系统；李雅普诺夫函数；稳定性

Abstract

This paper extends from the switched system and positive system to the switched positive system and discusses the one of the important properties of the system. focusing on the existence problem about a common linear copositive Lyapunov function for switched positive linear system, which consist of stable and pairwise commutable subsystems. The following three systems are considered here: only continuous-time subsystems, only discrete-time subsystems, mixed continuous- and discrete-time subsystems. It is demonstrated that a CLCLF can always be constructed whenever its subsystems are continuous-time, discrete-time or the mixed type. The case when the number of subsystems is two is first considered, then the obtained result is extended to the general case by using the mathematical induction method. Finally, using the numerical examples given by MATLAB to verify the validity of the results.

Key Words：switched system；positive system；Lyapunov function；stable

目录

第1章 绪论 1

1.1研究背景和意义 1

1.2切换系统、正系统及切换正系统的概念 2

1.3国内外研究现状 3

1.4本文研究的内容及章节安排 5

第2章 预备知识 7

2.1基本知识 7

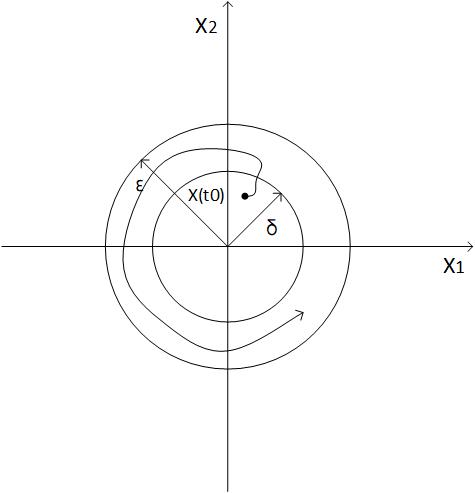
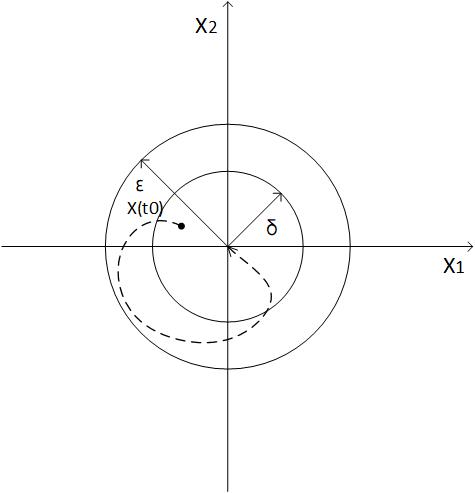
2.2 平衡状态的稳定性 10

2.3本章小结 12

第3章 切换正系统稳定性的证明 13

3.1 连续子系统稳定性证明 14

3.1.1两个连续子系统稳定性证明 14

3.1.2多个连续子系统稳定性证明 15

3.2 离散子系统稳定性证明 16

3.2.1两个离散子系统稳定性证明 17

3.2.2多个离散子系统稳定性证明 18

3.3 混合子系统稳定性证明 19

3.3.1 两个混合子系统稳定性证明 20

3.3.2 多个混合子系统稳定性证明 21

3.4 本章小结 22

第4章 切换正系统稳定性的验证 23

4.1 常微分方程的求解 23

4.2 MATLAB中程序编写 24

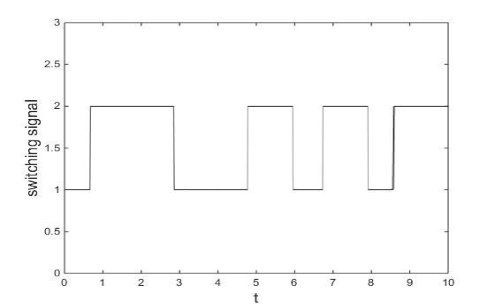
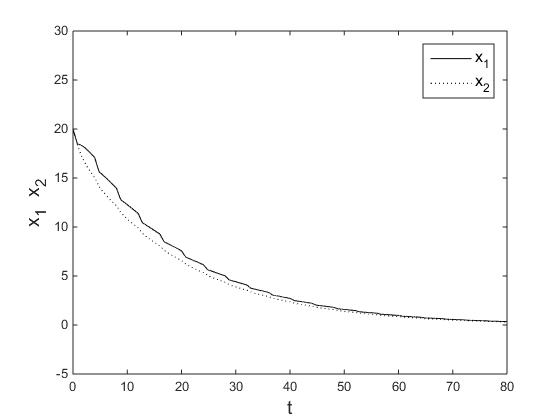
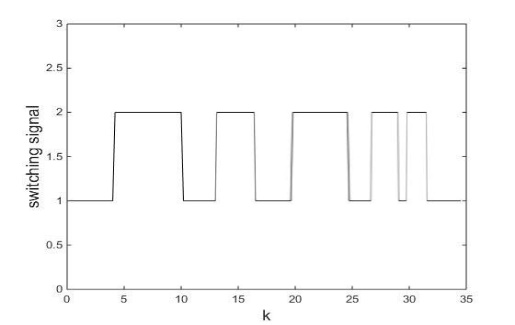
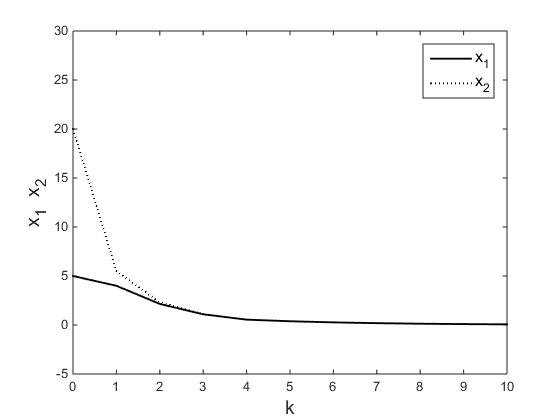
4.3在MATLAB中的仿真验证 25

4.4 本章小结 26

第5章 总结与展望 27

5.1 总结 27

5.2 展望 27

参考文献 29

致谢 31

1. 绪论

1.1研究背景和意义

控制是指在自然界存在的物理系统和人造系统的一些行为，可以按照操纵者的想法发生变化。而控制理论，是一门针对系统动力学以及控制方法的科学。他的发展大致是由三个部分组成：即由经典控制理论发展至现代控制理论，再达到智能控制理论。在经典控制理论中，通过本科的学习可以知道，其主要研究对象为单变量系统，且为描述其系统的输入输出特性，通常使用传递函数来表达。而对于现代控制理论而言，状态空间的引入是其最大的贡献，并在多变量系统的动力学中，利用状态方程对其进行了很好的描述，这令外界对系统内部的动态情况有了更好的了解。智能控制理论则是针对大量的非线性系统在工程实践中的应用，利用智能机器来模仿人的直觉和经验进行推理从而实现以上应用。然而跟随着社会的发展，人类在实际系统和工程应用中将面临更加复杂的情况，因此自然而然的将对控制理论提出更高的需求。现在，在控制领域内，复杂系统的建立和控制问题成为一个研究热点。作为描述较复杂系统动力学的一种有效方法，混杂系统理论为加深该系统的研究提供了一个很重要的途径。

在前文中所提到的混杂系统，是指一个系统中同时包括连续动态和离散动态并且两者之间存在交互行为的系统。在该系统中，利用微分方程来建立连续时间系统，而离散时间系统是由自由机、Petri等建立，由此也可以看出，混杂系统穿插着计算机科学和控制科学这两个学科的知识，因此具有非常重要的研究意义。而且在描述众多重要的被控对象时，例如复杂通讯网络、现代飞行编队、生物网络，混杂系统在这中间起着非常重要的作用。从1966年的混杂状态连续动态系统的论文发表以来，在过去的几十年中，混杂系统已获得了许多非常有价值的研究成果，并建立了相对完整的理论体系。

而切换系统作为混杂系统这个大家族中一个重要分支，因为其数学模型简单易懂并且广泛应用于工程实践中，所以受到控制界研究人员的重视。切换系统是指被一族子系统和一个在这些子系统中进行切换的切换信号所组成的系统。总结来说，切换系统在实际应用中的存在形式主要为两个方面。一方面为在自然界、社会和人造系统因为周遭的改变而变现出不相同的工作状态，例如，大型输电系统等。另一方面，在控制工程的实际应用中，面对一些结构复杂的系统，单一的控制器模式较难令系统达到全部的性能要求。所以在控制系统设计时也需要考虑利用多控制器的方法，由于本次毕业设计不涉及控制器的设计，所以在此不展开详细说明。

总结上述可知，因为切换信号的引入，导致包含切换系统的动力学变得复杂，在以整个系统为观察对象的情况下，可能出现单个子系统从未出现过的动态行为。那是因为在子系统稳定的情况下进行切换，整个系统不一定是稳定的；而在子系统不稳定的情况下进行切换，整个系统可以是稳定的。

1.2切换系统、正系统及切换正系统的概念

在过去的二十年中，研究领域对交换系统的稳定性分析和控制器设计越来越感兴趣，研究切换系统的动机也是多方面。众所周知，因为各种环境因素，许多实际系统本质上是多模式的，因此需要几个动态子系统来描述它们的行为。 由于这些系统本质上是切换系统，因此对切换系统的分析或设计是有助于处理实际系统。另一个重要的观察结果是，在指定系统的一组控制器之间进行切换可以看作是一个切换系统，以确保该系统在其他情况下无法得到证明的稳定性，实际上该切换已经用于自适应控制或改善自适应控制系统的瞬态响应。此外，智能控制设计的方法基于不同控制器之间切换的思想，因此，切换系统的研究对切换控制器和智能控制器的设计有很大的帮助。

切换系统实则是混杂系统中的一种，他是由子系统为连续时间或者离散时间以及控制系统间进行切换的切换信号组成。这里所提到的切换信号，也被称之为切换规则或切换率。在实际应用中，一般的切换信号取决于时间或状态两个元素，或者同时取决这两个元素。通常情况下，它的切换率是随机的。在混杂系统发展的这几十年来，针对切换系统的研究有很多，然而其主要的问题在于对系统的稳定性问题和构造问题。实际上，切换系统在实际生活中有着非常广泛应用，该系统的应用价值也被很好的体现出来了，例如网络控制系统、生物网络等。一般来说，系统运行的基本条件是系统稳定，而对于切换系统来说，若其子系统均为稳定，就切换系统整体而言，也存在稳定或不稳定两种情况。在切换系统中，若给予一个随机的切换规则，系统的稳定性可能变得不确定。因此在这类情况下，可以解决的方法是通过对切换信号的设计，从而令系统稳定。在实际应用中，切换信号存在许多种类，比较严格的一种是被称为平均驻留时间切换的切换信号。这种方法已经在许多的文章中被应用到了，而且是一种在稳定性分析中更为灵活的方式。

在自然界存在的物理系统和人造系统均有一类变量，取值总为非负值，例如在物理学中的物质密度、位移等，还有化学中反应物的浓度等。以上所提及的量均通过非负量来描述，在动力学系统中，对于这些系统，均可利用正系统来描述。近些年来，关于系统的一致性在复杂系统中的研究，涌现了许多由正系统组成的模型，在联合正系统理论后，可以对这些模型进行很好的处理。目前，许多研究人员都关注着正系统在动力学中的性质。

关于正系统，由于其起步较晚，在其研究初期，重点集中在对他的可观性和可控性上，这两个方面是大部分系统理论中所关注的。从而忽略了在动力学中的正系统的性质，例如稳定性和鲁棒性等。通过分析得出促使这一现象产生的原因在于：利用对于一般动力学系统的分析方法来分析正系统的相应性质。实际上这种方法存在的缺陷是，既不能很好的利用正系统的特性，也不能提出比较完善的解决方法。而对无时滞正系统的稳定性的研究，其结果再次令正系统的领域中研究热情被激发出来。目前，研究人员已经对具有各种特征的正系统展开了较为全面的研究，所取得的进展十分令人瞩目。发展至今，正系统的研究依旧让许多研究人员投身至此，目前大多数的目光都聚焦在线性正系统方面，该方面包含了该系统的稳定性、约束控制和控制器等方面。就稳定性而言，它是动力学系统最重要的性质之一，要想解决切换正系统的稳定性问题是需要寻找李雅普诺夫函数：1892年俄国学者李雅普诺夫针对稳定性，提出的稳定性理论，是一种较为严格且具有一般性的数学定义。此后，在学术界和工程界这两块领域对动力学系统中稳定性有了更多关注。众所周知的是，系统稳定是任何一个工程正常工作的前提条件，在研究一个动力学系统时，基本任务是首先判断他的稳定性。而在系统设计的过程看来，系统稳定性的重要性在于他是系统设计和综合的基础。在这其中，李雅普诺夫稳定性理论是确定系统稳定性的更一般理论，它利用的状态向量描述，不仅适用于单变量、线性、定常系统而且适用于多变量、非线性、时变系统。

此时将切换系统和正系统相结合，组成的切换正系统在实际生活中也十分广泛。在实际应用中会遇到各种问题，如切换系统运行过程中，由于某些原因出现不可避免的切换失灵，又或者，考虑到类似于机器人这种类型的系统，在实际应用中需要实现各个子系统间的切换，以上都是在切换正系统中需要考虑的实际问题。系统对于随机的切换策略是否均能稳定，即随机切换条件下的系统稳定性，都是在研究过程中不可忽略的问题。需要提出的是, 即使所有的子系统都稳定, 整个系统仍有可能不稳定。因此研究切换正系统的稳定性变得十分的重要。

1.3国内外研究现状

切换系统是混杂动力系统中的重要类别之一，该系统作为一种非常实用的模型，通常用来模拟一些具有切换性质的物理系统和人造系统。这些系统，通常来说是由连续时间子系统和离散时间子系统组成，并且存在一定的规则来协调这些系统的切换^[1]。在过去的十几年中，切换系统有了非常广泛的研究^[2]。由于切换系统的存在，这种系统的稳定性分析变得尤为重要^[3]。该系统的问题主要集中于任意切换条件和约束条件下的稳定性：前一个问题重点集中在寻找针对切换系统的一种共同李雅普诺夫函数^[4]。已经被证实的是，切换系统的共同二次李雅普诺夫函数与其子系统的交换性具有密切联系。在另一方面，就后一类切换系统而言，切换信号受到一些常规特性的限制。典型的约束切换信号的特征在于两个连续开关之间的平均时间不小于常数^[2]。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：