英语原文共 19 页

第五节 混凝土应力-应变曲线

钢筋混凝土构件的性能和强度受构件尺寸和形状以及混凝土和钢筋的应力应变特性的控制。本节讨论的应力-应变性能将在以后的章节中用于建立钢筋混凝土梁和柱的强度和性能的关系。

5.1 切线和割线弹性模量

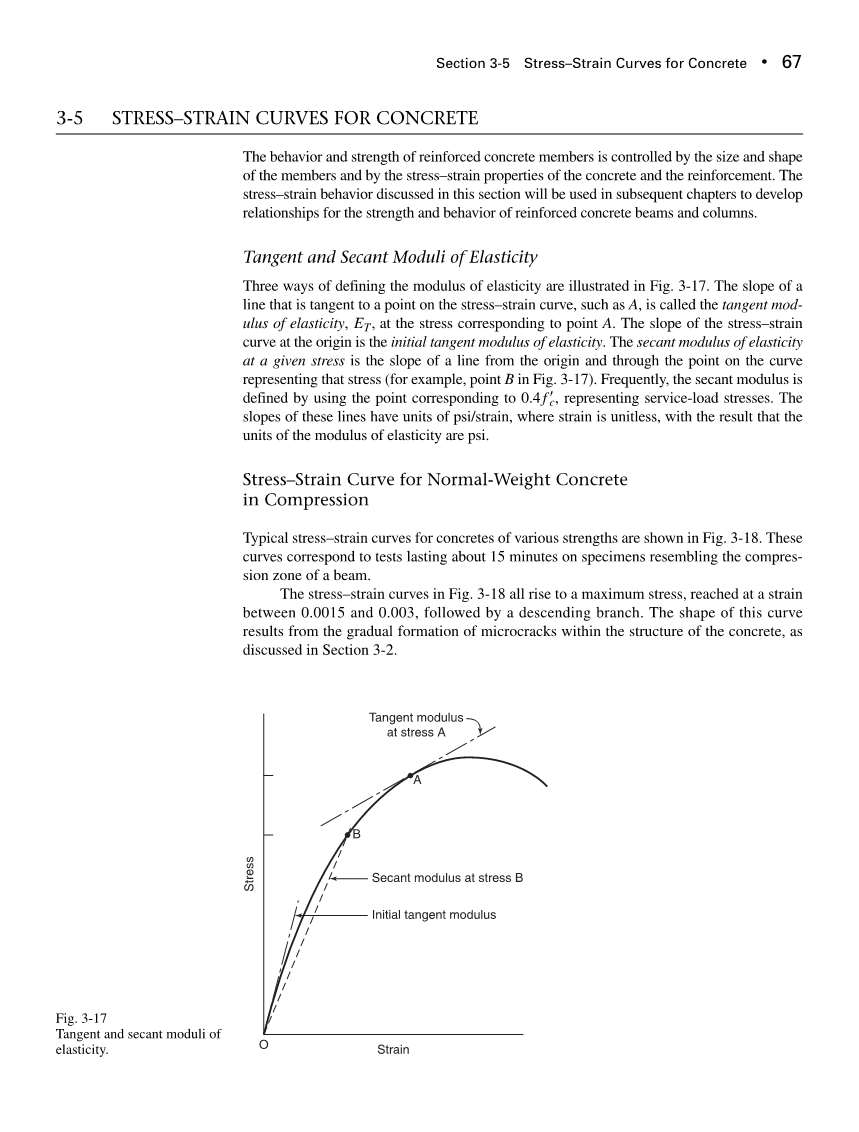
定义弹性模量的三种方法如图3-17所示。与应力-应变曲线上某一点相切的直线的斜率，如点A，称为A点对应的应力处切线弹性模量。应力-应变曲线在原点处的斜率为初始切线弹性模量。割线弹性模量是指在给定应力下，一条从原点到曲线上表示该应力的点的直线的斜率(例如图3-17中的B点)。通常，割线模量是使用荷载下对应于0.4fc^rsquo;的点来定义的。这些直线的斜率单位是psi/应变，其中应变是无单位的，因此弹性模量的单位是psi/应变。

5.2 普通混凝土受压应力-应变曲线

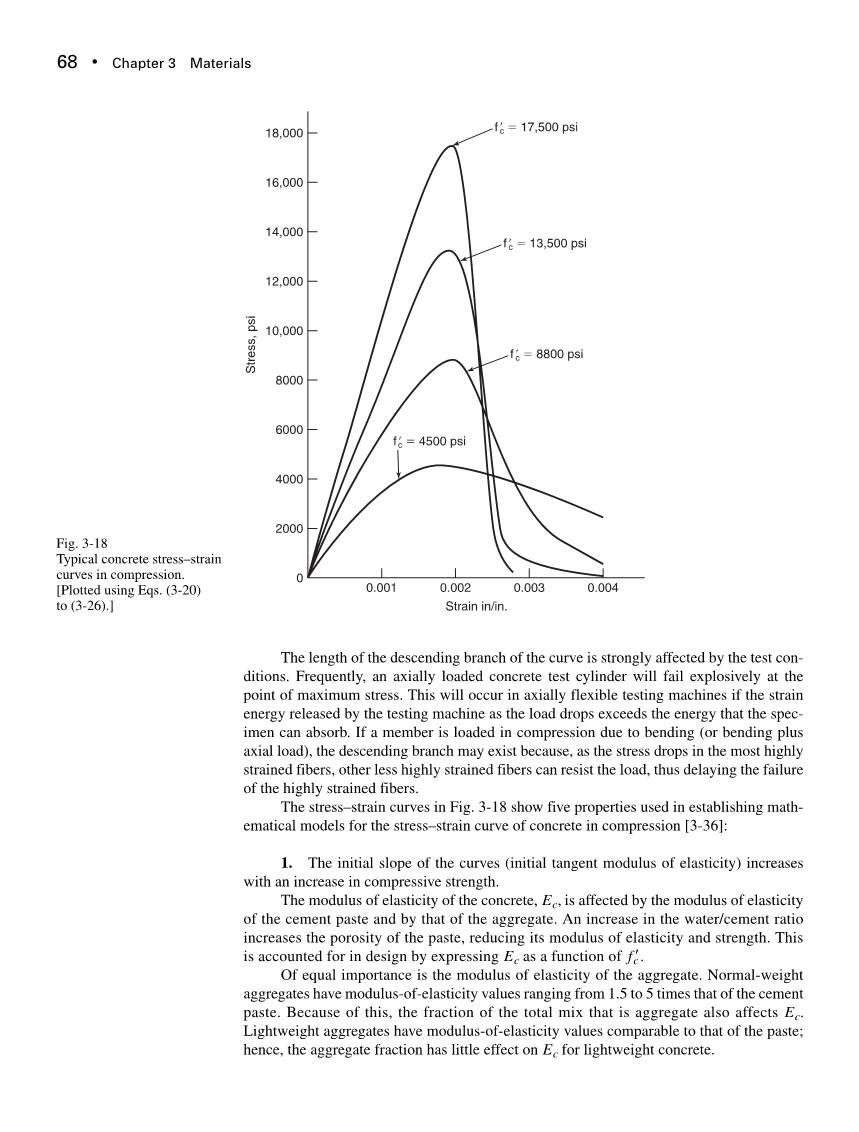
不同强度混凝土的典型应力-应变曲线如图3-18所示。这些曲线反应的是在梁的受压区持续受荷约15分钟所得到的结果。

图3-18所示的应力-应变曲线，应变在0.0015 ~ 0.003之间，均上升至最大应力，随之下降。该曲线的形状是混凝土结构内部微裂缝的逐渐形成而产生的结果，如第3-2节所述。

图3-1 切线和割线模量

图3-1 应力-应变曲线

试验条件对曲线下降段的长度影响较大。通常，轴向加载的混凝土试件会在最大应力点发生破碎而失效。如果负载下降时试验机释放的应变能超过试样可吸收的能量，则在轴向柔性试验机中会发生这种情况。如果一个构件由于弯曲而受压(或弯曲加上轴向载荷)，则可能存在下降段，因为当应力在高应变纤维中下降时，其他低应变纤维可以抵抗载荷，从而延缓高应变纤维的破坏。

图3-18所示的应力-应变曲线显示了建立受压混凝土应力-应变曲线数学模型的5个特性[3-36]:

5.2.1 曲线的初始斜率(初始切线弹性模量)随着抗压强度的增大而增大

混凝土的弹性模量受水泥浆体和骨料的弹性模量的影响。

混凝土的弹性模量E_c受水泥浆的弹性模量和骨料的弹性模量的影响。 水/水泥比的增加增加了浆料的孔隙率，降低了其弹性模量和强度。这通过在设计中将E_c表示为f_c的函数来解释的。

同样重要的是骨料的弹性模量。相同重量的骨料的弹性模量是水泥石的1.5 ~ 5倍。正因为如此，总混合物中骨料所占的比例也会受到影响E_c。轻质骨料的弹性模量与浆料相当；因此，对于轻质混凝土，骨料所占比例对E_c的影响很小。

混凝土的弹性模量经常采用ACI规范第8.5.1节的规定，即:

psi （3-17）

式中 w是混凝土的重量，单位是lb/ft3。该等式是通过对密度为90至155 lb/ft3的混凝土进行短期试验而得出的，其值相当于0.50 f₀rsquo; [3-37]下的割线弹性模量。初始切线模量大约高大10%。因为该等式忽略了骨料的类型，所以数据的分散性很大。式 (3-17) 主要考虑的是低模量集料普遍存在的部分。如果在设计中对挠度或振动特性要求较高，则使用混凝土时需重新测定其E_c。

对于密度为145 lb / ft3的普通混凝土，ACI规范第8.5.1节给出了其弹性模量，即：

psi （3-18）

ACI委员会363[3-8] 提出了以下高强度混凝土的计算公式：

psi （3-19）

5.2.2 应力-应变曲线的上升部分类似于抛物线，其顶点在最大应力处。

为了便于计算，曲线的上升部分经常近似为抛物线[3-36]、[3-38]和[3-39]。随着混凝土强度的增加，曲线趋于变直[3-40]。

5.2.3 随着混凝土强度的增加，最大应力处的应变也随之增大。

5.2.4 如第3-2节所述，应力-应变曲线下降段的斜率是由于混凝土微观裂纹的扩展和整体开裂而导致的混凝土结构破坏所致。

对于强度高达6000 psi的混凝土，应力-应变曲线下降段的变化往往比上升段平缓。下降段的斜率随混凝土强度的增加而增大，如图3-18所示。对于大于10000psi的混凝土，下降段是一条几乎垂直、不连续的“曲线”，这是因为混凝土的破坏主要为纵向裂缝破坏。

5.2.5 达到最大应变后，极限应变随混凝土强度的增加而减小。

达到最大应力后，应力-应变曲线的下降部分变化很大，很大程度上取决于试验程序。同样，最大应变或极限应变也很大程度上取决于试样类型、载荷类型和试验速率。在高荷载下，荷载重分布的可能性较大时，极限应变往往较高。在弯曲试验中，测量了0.0025到0.006之间的值。

压应力-应变图方程

图3-19 混凝土压缩应力-应变曲线的解析近似

对于强度在6000psi左右的混凝土，应力-应变曲线的一种常见表示方法是修改后的Hognestad应力-应变曲线，如图3-19a所示。它一条二阶抛物线组成和一条向下倾斜的线组成，抛物线顶点处的应变为，其中，下降段的应力和极限极限应变分别为和0.0038[3-38]。式(3-14)描述了一个二阶抛物线，其顶点在处。降低的强度，这说明了圆柱体试件和标准试件强度之间的差异。这些差异是由于不同的养护条件和浇筑方式造成的，由于水的垂直迁移，这将会加剧不同的增水效果，并且增大快速加载的圆柱体试件的强度与缓慢加载的相同混凝土的强度之间的差异，如图3-2所示。

应力-应变曲线的另外两个表达式也将给出。如图3-19b所示的应力-应变曲线，由于整个应力-应变曲线是一个连续的函数，因此在涉及混凝土强度高达6000psi左右的分析研究中使用起来很方便。对于到达5000psi左右，时，曲线上的最高点的应力取，其反应的应力图性质与4-3节中所述的矩形应力图性质相似。最大应力对应的应变，可以认为等于。

为任意应变，令，任意应变下的应力为：

（3-20）

对于等宽压缩区，应变由0到的应力图形的平均应力为，其中：

（3-21）

应变由0到的应力图形的重心与所在点的距离为，其中：

（3-22）

式中：计算时以弧度表示。对于当应变大于时，应力-应变呈逐渐下降趋势的混凝土，其应力-应变曲线是偏于理想的。因此，它适用于达到5000psi左右的普通混凝土和达到4000psi左右的轻质混凝土。

Popovics[3-40]综述了混凝土压缩应力-应变曲线的表达式。Thorenfeldt、Tomaszewicz和Jensen[3-42]将其中两个表达式进行了推广，得到了适用于强度为15 ~ 125mpa的混凝土的应力-应变曲线。应力与相应应变的关系为：

柱体试验获得的峰值应力；

（3-23）

式中 = =达到时的应变（见等式（3-27））；

= 曲线拟合系数等于（见等式（3-24））；

= 初始切线模量（当时）；

；

k = 控制应力-应变曲线上升段斜率和下降段斜率的系数，小于1.0时取1.0，大于1.0时取大于1.0的实际值。[见等式（3-25）和（3-26）]

这四个常数、、和k可以直接从混凝土的应力-应变曲线中推导出来（如果能）。如果不能，可以从由Collins和Mitchell[3-43]推到的公式(3-25)~(3-27)中计算出来。方程(3-17)和(3-18)可用于计算，尽管它们是从通过原点和0.4~0.5之间对应的点导出的割线模量。

对于正常密度的混凝土：

（3-24）

式中 的单位是 psi;

当时：

k = 1.0 （3-25）

当时：

(psi) （3-26）

如果n、和已知，峰值应力下的应变可以由下式计算：

（3-27）

由式(3-23)计算得到的应力-应变曲线族如图3-18所示。式(3-23)为光滑连续的下降段。实际上，随着混凝土结构的破坏，高强混凝土的下降段往往会出现一系列的锯齿状台阶。方程3-23用光滑曲线逼近，如图3-18所示。

一般地，设计中使用的等效应力图直接基于应力-应变曲线，该曲线峰值应力等于，这是为了考虑到实际强度和圆柱体抗压强度之间的差异。为了预测实验结果，可通过统计计算应力-应变曲线的纵坐标值，然后乘以0.90。所以，对于基于应力-应变关系的设计，可由和纵坐标分别乘以0.90得到应力-应变曲线。

如图3-15所示，侧向围压会使混凝土抗压强度增大，破坏应变也将增大。约束混凝土的附加强度和延性主要用于地震区结构的铰接区域。约束混凝土的应力-应变曲线如[3-44]所述。当压缩试样加载、卸载和重新加载时，其应力-应变响应如图3-20所示。该曲线的包络线非常接近单轴试验的应力-应变曲线。卸载后混凝土中残留的大量残余应变表明，非弹性响应是由混凝土内部结构的损坏引起的，正如前面提出的微裂纹理论所述的那样。

5.3 普通混凝土受拉应力-应变曲线

轴向受拉混凝土的应力-应变响应可分为两阶段。在最大应力之前，应力-应变关系呈微曲。拉伸强度的50%左右之前，关系曲线是线性的。纯拉伸时的峰值应变约为0.0001，弯曲时的峰值应变约为0.00014 ~ 0.0002。应力-应变曲线的上升部分可以近似为斜率为的直线，最大应力等于抗拉强度，也可以近似为一条抛物线，最大应变，最大拉应力为。后一条曲线的和如图3-21a所示，其值可以由等式（3-11）和（3-18）得到。

在达到抗拉强度后，在靠近最大拉应力点的开裂区出现微裂纹，随着伸长量的继续增加，混凝土的抗拉能力急剧下降。在这一阶段的性能，伸长集中在断裂过程中，而其余的混凝土为卸载弹性。卸载效应最好用应力-裂纹-开裂-展开图来描述，如图3-21b所示的两条理想直线。图中所示的裂缝宽度大小是合适的，但具体值取决于实际情况。当裂纹完全形成时，拉伸能力降为零。这一过程发生在一个非常小的裂缝宽度处。[3-46]给出了更详细的讨论。

5.4 泊松比

在临界应力以下(见图3-1)，混凝土泊松比在0.11 ~ 0.21之间变化，一般在0.15 ~ 0.20之间。基于双向加载混凝土试验，Kupfer等人[3-32]在报告指出：单向或双向受压的混凝土，其泊松比为0.20；单向或双向受拉的混凝土，其泊松比为0.18；既受拉又受压得的混凝土，其泊松比在0.18 ~ 0.20之间。在持续受荷作用下泊松比近似保持不变。

第六节 随时间变化的体积

混凝土的体积变化主要有三种，即收缩、徐变和热膨冷缩，这些变化都可能使混凝土产生应力、开裂或挠度变形，从而影响钢筋混凝土结构的使用性能。

6.1 收缩

收缩是指混凝土在恒定温度下硬化和干燥过程中体积减小的现象。收缩量随时间的增加而增大，如图3-22a所示。

收缩的主要类型包括干燥收缩或一般收缩。收缩是由于凝胶颗粒表面的一层吸附水(电结合水分子)损失造成的。该层大约只有一个水分子那么厚，差不多是凝胶颗粒大小的1%。游离的未吸附水的损失对收缩的大小影响不大。

收缩应变与相对湿度有关，当相对湿度小于或等于40%时，收缩应变可达到最大值。在重新润湿混凝土后收缩可以部分恢复。并且由于收缩应变的变化，暴露在季节性湿度变化中的结构可能会轻微膨胀和收缩。

收缩应变的大小也取决于混凝土的配合比和所用水泥的类型。硬化的水泥浆体收缩，而骨料起到抑制收缩的作用。因此，由硬化水泥浆体组成的混凝土的体积分数越大，收缩也就越大。这对于普遍使用的自固结混凝土尤为重要，因为通常情况下自固结混凝土的浆体含量比强度相同的固结混凝土高得多。水灰比或水泥总量的增加会降低骨料的体积，从而减少骨料收缩的约束。此外，较细的水泥具有较大的表面积比，因此，在收缩期间吸附水的损失将更多。由于石英和花岗岩的弹性模量较高，用石英或花岗岩骨料制成的混凝土比用砂岩骨料制成的混凝土收缩小。

图3-22 应变-时间曲线

当水分从混凝土中扩散出来时，就会发生干燥收缩。结果，外部比内部收缩得更快，这将导致混凝土的外部产生拉应力和内部产生压应力。对于大型构件，随着体表比的增加，收缩会减少，因为有更多的潮湿混凝土来抑制收缩。所以在大型构件中，收缩速率也较慢。

由于水泥基体内部的水化反应，

资料编号：[3468]