英语原文共 6 页，剩余内容已隐藏，支付完成后下载完整资料

---

Dawson，EM，Roth，WH＆Drescher，A。（1999）。 Ge#39;technique 49，No.6,835-840

减少强度的边坡稳定性分析

E.M. DAWSON，*W.H. ROTH*和A. DRESCHERt

关键词：堤防; 山体滑坡; 极限状态设计分析; 数值模拟和分析; 可塑性; 连续下坡。

介绍

对于斜坡，安全系数F传统上定义为实际土体抗剪强度与防止破坏所需的最小抗剪强度之比（Bishop，1955）。 正如Duncan（1996）所指出的那样，F是土壤抗剪强度必须被分开的因素，以使边坡达到失效的边缘。 由于它被定义为剪切强度折减系数，因此用有限元或有限差分程序计算F的一个显而易见的方法就是简单地降低土的抗剪强度直到发生崩塌。 所得到的安全系数是土体的实际抗剪强度与破坏时减小的抗剪强度之比。 这种“剪切强度降低技术”早在1975年由Zienkiewicz等人使用。 （1975年），现在已被Naylor（1982），Donald＆Giam（1988），Matsui＆San（1992），Ugai（1989），Ugai＆Leshchinsky（1995）等人应用。

剪切强度降低技术有一个

数量优于切片法用于边坡稳定性分析的优点。 最重要的是，关键破坏面自动发现。 由于需要较长的计算机运行时间，所以该技术的应用在过去受到限制。 但随着台式计算机日益增长的速度，该技术正在成为切片切片方法的一种合理替代方法，并且越来越多地被用于工程实践中。 但是，这项技术的准确性几乎没有调查。 本文将采用剪切强度降低技术获得的安全系数与均质路堤的极限分析解进行比较。

显式有限差分法

使用显式有限差分代码FLAC（Itasca Consult-

手稿于1999年2月9日收到; 修订稿于1999年8月13日接受。

关于本文的讨论于2000年6月30日结束; 欲了解更多详情， II。

*Dames＆Moore，洛杉矶。

明尼阿波利斯明尼苏达大学。

835

1995年）。 对于给定的单元形状函数，由FLAC求解的代数方程组与用有限元方法求解的代数方程组相同。 然而，在FLAC中，这组方程是使用动态松弛（Otter et al。，1966）解决的，这是一个明确的时间推进过程，其中完整的动态运动方程逐步整合。 静态解决方案通过包含阻尼项来逐步消除系统的动能。

FLAC的收敛标准是节点不平衡力，即从其相邻元素作用在节点上的力的总和。 如果一个节点处于平衡状态，这些力总和应为零。 对于这项研究，每个节点的不平衡力通过作用在该节点上的引力体力来标准化。 当网格中每个节点的归一化不平衡力小于10^-3时，仿真被认为已经收敛。

极限分析解决方案

陈（1975）提出了极限分析，均质路堤稳定性的上界解，假设对数螺旋破坏面。 陈的解决方案扩展到包括Michalowski（1995a，1995b）的孔隙压力的影响。 这些解以无量纲稳定值N_S的形式给出

(1)

其中H_C是具有土壤单位重量y和内聚力C的斜坡的临界高度.N_S的值针对坡度角f3（来自水平面），摩擦角alpha;和孔隙压力系数r_u。 Bishop（1954）提出的孔隙压力系数将孔隙压力定义为上覆应力的一部分。 在地面以下的深度z处的孔隙压力u由下式给出

u = r_uyz (2)

示例稳定性分析

考虑一个高度均匀的堤岸

3摩擦角cent;= 20°，单位重量y = 20 kN / m，角度beta; = 45°倾斜，

根据Chen（1975）的极限分析方法，对于这些土壤属性，斜率的安全系数恰好为1.0。

= =

FLAC在平面应变下模拟路堤，采用小应变模式（节点坐标不根据计算的节点位移进行更新）。 土壤被模拟为具有莫尔 - 库仑屈服条件和相关流动法则的线性弹性完全塑性材料。 显示数值网格

0.5

0.4

标准化的不平衡力

0.3

0.2

0.1

0.0

-0.1 .

. . . .

. . .

在图1中，有20个元素宽，20个元素高。 沿着左右边界的节点的水平位移是固定的，而水平和垂直位移沿着底部边界是固定的。

为了用剪切强度降低技术进行边坡稳定性分析，对一系列安全性试验因子F^审讯进行模拟，其中根据等式

0 80 0 85 0 90 0 95 0 100 1 05 1 10 1 15

试用安全因素

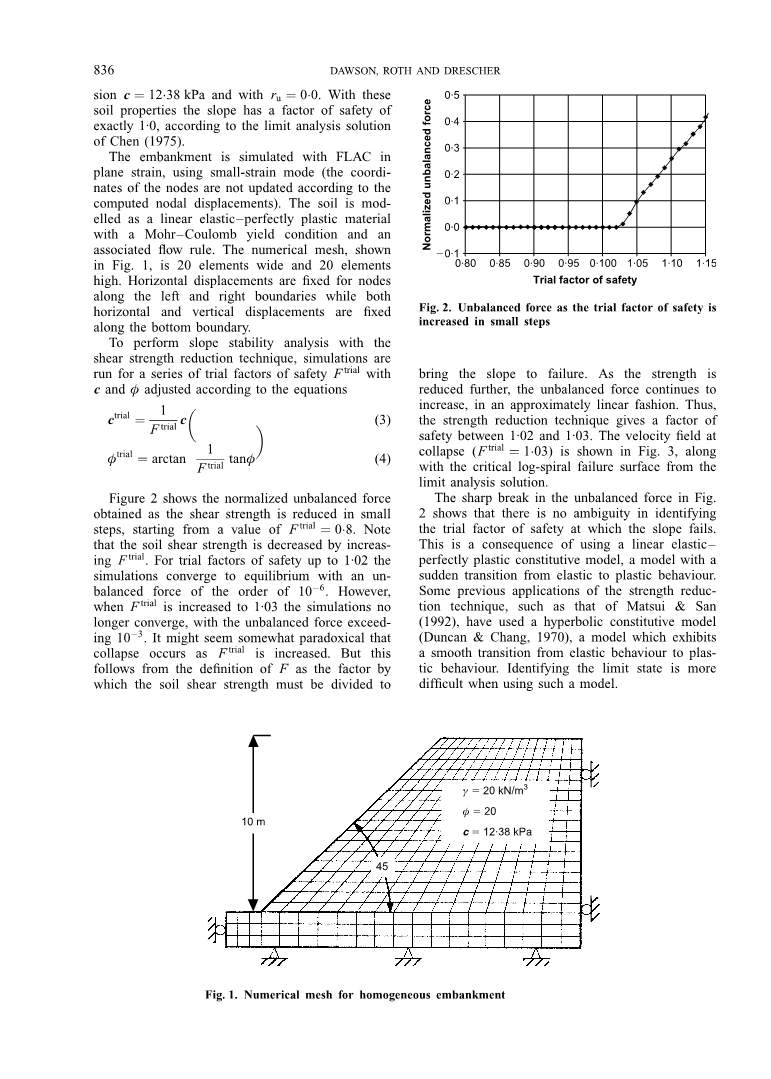
图2.不平衡的力量作为安全的试验因子以小的步幅增加

使斜坡失败。 随着力量进一步减弱，不平衡的力量继续存在

Ctrial

1

=FtrialC (3)

以近似线性的方式增加。 因此，强度降低技术给出了1·02和1·03之间的安全系数。 速度场在

(4)

图2显示了从F^审讯0 8的值开始，剪切强度以小阶跃降低时得到的归一化不平衡力。注意，通过增加F^审讯，土壤抗剪强度降低。 为了试验安全系数达到1.02，模拟会以大约10^-6的不平衡力收敛到平衡。 然而，当F^trial增加到1.03时，模拟不再收敛，不平衡力超过10^-3。 当F^审讯增加时，崩溃发生似乎有些矛盾。 但这是从F的定义作为土壤抗剪强度必须被分配到的因素

=

崩溃（F^trial103）与极限分析解决方案中的临界对数螺旋破坏面一起显示在图3中。

图2中不平衡力的急剧中断表明，在确定斜坡失效时的安全试验系数时不存在模棱两可的问题。 这是使用线性弹性理想塑性本构模型的结果，该模型是从弹性到塑性行为突然转变的模型。 先前的一些强度降低技术的应用，例如Matsui＆San（1992）的应用，已经使用了双曲本构模型（Duncan＆Chang，1970），该模型展现了从弹性行为到塑性的平滑过渡行为。 使用这种模型时，识别极限状态更加困难。

=

10 m

gamma;= 20kN / m³

phi; = 20

c = 12.38kPa

45

图1.均质路堤的数值网格

临界对数螺旋曲面

图3.崩塌时的速度场以及临界对数螺旋曲面

使用包围和等分可以更有效地找到发生塌陷的F^审讯的值。 首先建立上下括号。 最初的较低括号是模拟收敛的任何F^审讯。 最初的上限是任何F^审讯，模拟不收敛。 接下来，测试上支架和下支架之间的中点。 如果模拟收敛，则下部支架将被这个新值所取代。 如果模拟没有收敛，则更换上部支架。 重复该过程直到上下括号之间的差值小于指定的容差。

基准研究

为了评估强度降低技术的准确性，对各种参数进行了模拟。 路堤采用从15°到90°范围内的倾斜角f3进行模拟。 土壤的风速值范围为10°至40°，r_u值为0·0,0·25和0·5。 对于f3，cent;和r_u的每个组合，Chen（1975）或Michalowski（1995a）给出的稳定性数字用于计算坡度高度，内聚力和单位重量的组合，使得堤坝具有正好1.0的安全性。

在实践中，莫尔 - 库仑屈服条件

往往与张力切断相结合（Chen，1975）。 为了与极限分析解决方案进行比较，此处未使用张力截止值。 相反，Mohr-Coulomb屈服条件假定在拉伸正应力范围内是有效的。 换句话说，破坏包络与c / tancent;处的法向应力轴相交。 如果使用零张力截断值，使得土壤的单轴抗拉强度为零，则路堤的顶部发生拉伸破坏，计算的安全系数降低几个百分点。

-

模拟运行两个细网格

（60times;60个元素）和一个粗糙网格（20times;20个元素）。 通过连续的包围和等分计算安全因素，直到上下括号之间的差异小于4times;10^-4。 报告的安全系数是最终上下括号的平均值。 表1给出了计算r_u0 0的安全系数，而表2给出了r_u0 25的安全系数，r_u0 5的安全系数列于表3。安全因素一般在极限分析解决方案的几个百分点内。 对于较陡的斜坡和较高的摩擦角度，差异最大。 如所预期的那样，细网格比粗网格产生更好的结果。

两个例外与该公司的密切协议有关

=

=

=

极限分析解是针对r_u0 25和r_u0 50（参见表2和3的最后一行）的垂直斜率（f3 90°）。 由于高孔隙压力（ur_uy H）和零水平总应力的组合，这里的模拟失败在斜坡的脚趾处。 例如，对于r_u0 50，脚趾斜面处的孔隙压力超过土壤抗拉强度。

=

=

= = =

为进行图形比较，用稳定性数字表示数值结果很方便。 使用等式（1）和（3）可以找到对应于计算的安全系数的稳定性数字。 对于r_u0 0情况（表1），图4和5中的稳定性数字相对于土壤摩擦角绘制。 图4显示了粗网格的强度降低结果，而图5显示了细网格的结果。 随着网格的细化，强度降低结果似乎收敛到极限分析解决方案。

=

结论

已经用强度降低技术计算的安全边坡稳定性因素与基于对数螺旋破坏机制的上限极限分析解决方案进行了比较。 对各种倾斜角，土壤摩擦角和孔隙压力系数进行分析。 如果数值网格充分精确，安全强度降低因子在极限分析解决方案的几个百分比范围内。 强度降低结果通常略高于极限分析预测的结果。 严格地说，获得的密切协议并不能证明强度降低技术的准确性，因为极限分析解决方案是一个上限。 尽管如此，通过完全不同的方法获得的两种解决方案之间的相似性支持了广泛持有的观点，即对数螺旋解决方案实际上是一个确切的解决方案。 如果这是真的，那么期望数值解答稍微有点合理

表1.安全计算因子（r_u= 0·0）

坡度角，f3	摩擦角度， cent;	稳定性编号 NS= HC（y / C） （来自Chen，1975）	因子	的		安全
			细网格		粗网
15	5	14·38	1·002		1·023
	10	45·49	1·003		1·027
30	10	13·50	1·006		1·034
	15 lt; 全文共7131字，剩余内容已隐藏，支付完成后下载完整资料 资料编号：[8837]，资料为PDF文档或Word文档，PDF文档可免费转换为Word