神经网络求解TSP问题的研究毕业论文
2020-04-04 12:51:52
摘 要
一直以来,TSP问题都是组合优化领域之中不能忽视的重要研究对象之一。七十年代中期的计算复杂性理论以及数学规划的出现和发展则对于组合优化问题的发展起了很大的作用。前者表明了,TSP问题这个被称作NP完全的问题在计算上与其他类似的组合优化问题是等价,即不可以用已知的多项式的算法去求解此问题。由此可知,最优化方法能力是有限的,我们需要寻找更完善的解决方法。这时候,人工神经网络的出现和发展为问题的解决提供了全新的思路。
本文详细的介绍了TSP问题的具体描述、数学模型和现阶段已存在的解决TSP算法。接着对反馈式神经网络,即离散型Hopfield神经网络与连续型Hopfield神经网络的拓扑结构、数学模型及稳定性也进行了阐述。可以知道,离散型Hopfield神经网络在联想记忆领域得到广泛应用,而连续型Hopfield神经网络则在优化计算方面被应用,故本文详述了连续型Hopfield神经网络解决TSP问题的理论过程,并用MATLAB和LINGO两个软件进行了仿真求解。
关键词:旅行商问题(TSP);人工神经网络 ;Hopfield神经网络
Abstract
The TSP problem has always been one of the important research objects in the field of combinatorial optimization.In the mid-1970s, the theory of computational complexity and the emergence and development of mathematical programming played a very important role in the development of combinatorial optimization problems.The former shows, TSP problem this known as the np-complete problems in calculation and other similar combinatorial optimization problem is equivalent to that no known polynomial algorithm to solve this problem.Therefore, the optimization method is limited, and we need to find a better solution.At this time, the emergence and development of artificial neural network provide a whole new way of thinking.
In this paper, the specific description of TSP problem, the mathematical model and the existing solution of TSP algorithm are introduced in detail.Then the topology, mathematical model and stability of the feedback neural network, namely the discrete Hopfield neural network and the continuous Hopfield neural network, are also described.Can know, discrete Hopfield neural network is widely applied in the field of associative memory, while continuous Hopfield neural network is applied in optimization calculation, this paper details the continuous Hopfield neural network theory to solve the problem of the TSP process, are simulated with MATLAB and LINGO software solution.
Key words:Traveling salesman problem (TSP); artificial neural network; Hopfield neural network
目录
第1章 绪论 1
1.1研究背景及意义 1
1.1.1研究背景 1
1.1.2研究的意义 1
1.2国内外研究现状 2
1.2.1国外研究现状 2
1.2.2国内研究现状 3
1.3论文研究内容及技术路线 4
1.3.1研究内容 4
1.3.2研究目标 4
1.3.3技术路线 4
1.4本章小结 4
第2章TSP问题 5
2.1 TSP问题简述 5
2.2 TSP问题的数学模型 5
2.3 TSP问题求解算法综述 6
2.3.1精确算法 7
2.3.2近似算法和启发式算法 8
2.3.2.1近似算法 8
2.3.2.2启发式算法 8
2.3.3 分枝割平面算法 9
2.4 本章小结 9
第3章人工神经网络 10
3.1人工神经网络简述 10
3.1.1 人工神经网络简介 10
3.1.2神经元的数学模型 11
3.1.3反馈式神经网络 12
3.2 离散型Hopfield神经网络 12
3.2.1神经网络的结构和工作方式 12
3.2.2神经网络的稳定性 13
3.2.3能量函数 15
3.3 连续型Hopfield神经网络 17
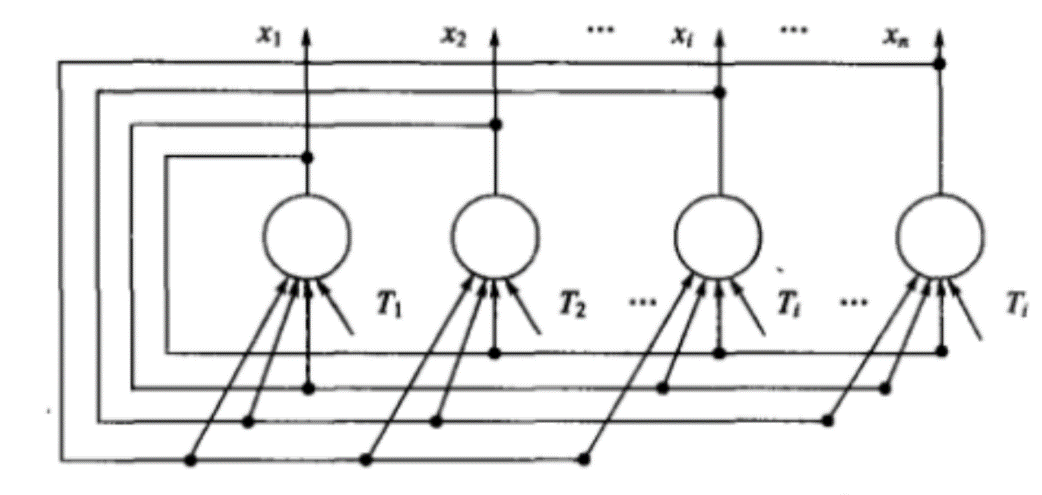
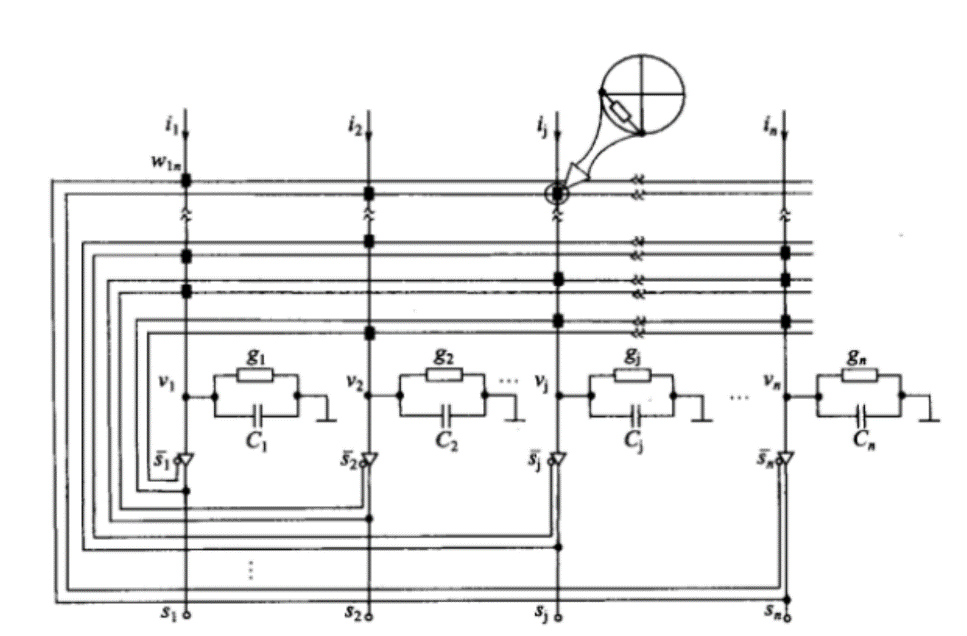
3.3.1神经网络的拓扑结构 17
3.3.2神经网络的稳定性和能量函数 18
3.4 Hopfield神经网络应用 20
3.4.1离散型Hopfield神经网络解决联想记忆问题 20
3.4.2连续型Hopfield神经网络解决优化计算问题 20
3.5 本章小结 20
第4章 神经网络解决TSP问题 21
4.1 连续型Hopfield神经网络解决TSP 21
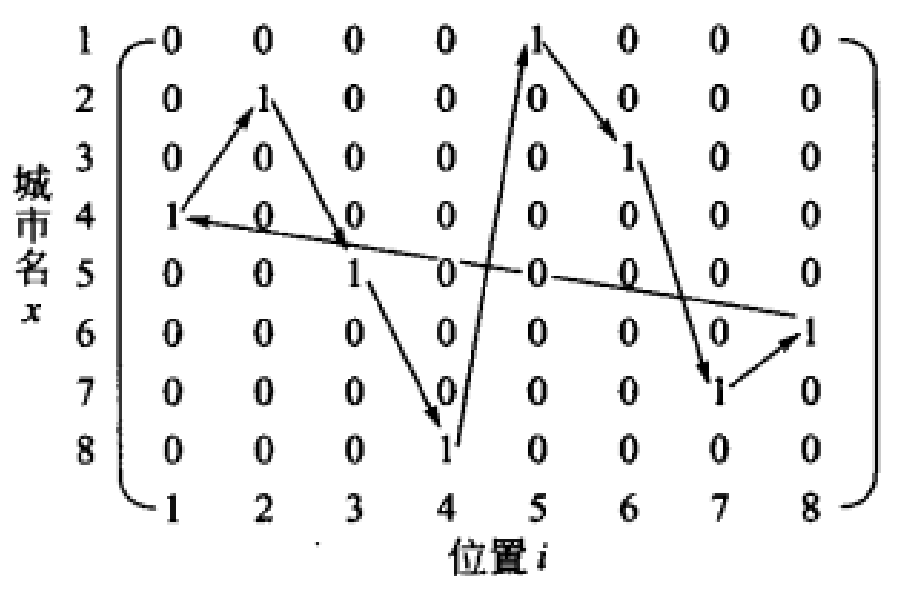
4.1.1问题描述 21
4.1.2能量函数设计 22
4.2 解决TSP问题实例 24
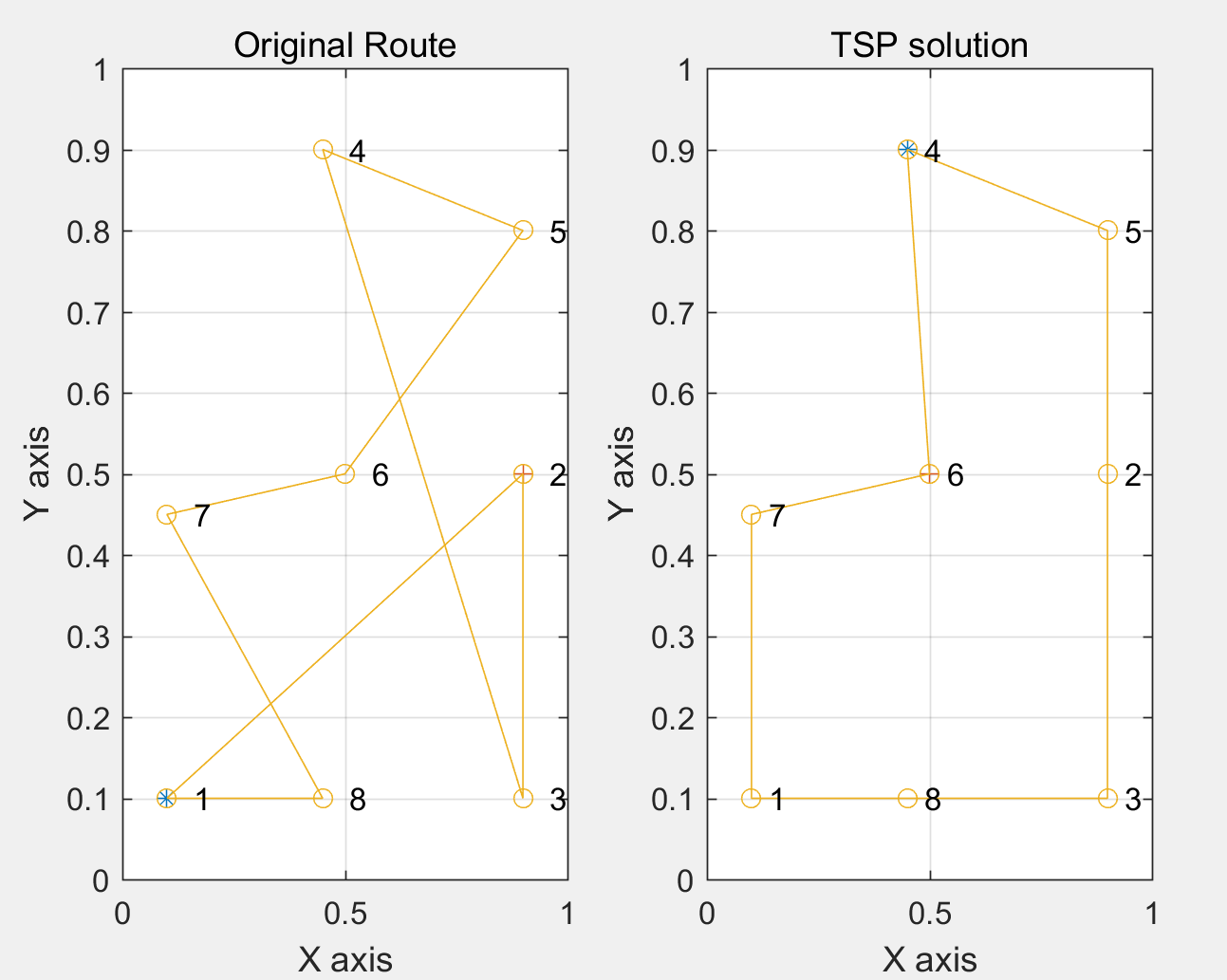
4.2.1用MATLAB解决TSP问题 24
4.2.2用LINGO解决TSP问题 26
4.2.3 MATLAB和LINGO解法对比 26
4.3 本章小结 26
第5章 总结与展望 27
5.1 总结 27
5.2 展望 27
5.3 经济性与环保性分析 27
附录 28
参考文献 29
致谢 31
第1章 绪论
1.1研究背景及意义
1.1.1研究背景
TSP问题(Traveling Salesman Problem),我们也常常把其称为旅行销售员问题,或者是邮递员路径问题。它作为组合优化领域中一个十分经典的问题,也是运筹学研究中一个不可避免的问题,它可被描述为:一旅行商欲遍历平面上的N个城市,他对每座城市仅能访问一次且终点必须回到出发的城市,那么按照怎样的城市访问顺序可以使回路长度最短。虽然TSP问题陈述起来十分简单,但求解起来却并非如此。TSP问题不仅仅是一种问题的集中体现,而是生产和生活中很多问题的代表,它广泛存在于我们的生活当中,所以提出一种高效解决TSP问题的方法是具有理论和实际意义的。当TSP问题中的城市数较少时,通常用枚举法等方法去解决,但当城市数量较大时,比如说当城市数量为n时,则可能的路径数量达到了n!/2n,此时从理论上看,用枚举法去一一列举可能存在的路径就显得工作量巨大而且不切实际,所以一种精度较高而且计算时间短的算法是十分必要的[1]。
1.1.2研究的意义
“神经网络”是兴起于20世纪80年代的,人工智能领域的研究热点,通常指用大量的神经元(即简单的计算单元)所构成非线性的系统。在一定的层次上,神经网络对人脑神经系统的各种各样的性能和功能进行模仿,这也使其具有学习、记忆和计算等一系列智能处理功能。同时,它还有着如下的一些能力和特点:可以实现非线性映射;不需要精确的数学模型;擅长于从输入输出数据中筛选有用的内容;易于实现并行计算;易于硬件和软件实现。近十年来,人工神经网络的研究工作进步了很多。在模式识别、预测估计、自动控制等领域已经成功地解决了很多我们用计算机都没办法去解决的实际问题。人工神经网络包括了Hopfield网络、BP网络、自组织特征映射网络等典型网络。Hopfield神经网络( HNN )是广泛被应用于求解组合优化问题的一种神经网络模型,利用Hopfield网络求解组合优化问题时,我们用的求解的方法是:将目标函数转化为网络的能量函数,然后把求解的变量对应网络的状态。当网络的能量函数收敛到最小值时,问题的最优解就会得到解决。我们可以知道神经网络呦一个特点,那就是它计算时是并行的,所以可以不用担心会出现指数“爆炸”这样一种情况。
1.2国内外研究现状
TSP一直是组合优化中最活跃的研究课题之一。全世界的科学家一直在力图创新并解决TSP问题。而对于TSP问题,人们最先想到的就是穷举法。但是采用穷举法时最优解的存在是有前提的,那就是当问题规模较小,即可行解的数量有限的时候。但是倘若可行解集合中的有限点数目逐渐增多时,此种方法则是不可取的。随着n的不断增长,函数将出现“指数爆炸”现象[2]。故TSP在算法复杂性[3]上遵循的是指数时间算法,则穷举法不能适应大规模的TSP的问题。
穷举法在被应用的时候,其计算时间和计算难度随着问题的复杂化也会不断增加,人工计数与计算机运算在庞大的计算量面前显得捉襟见肘。鉴于上述情况,有一种在最优算法基础上进行了修改之后,再次被提出的启发式算法的定义由文献[4]给出:启发式算法是一种在可接受的计算费用内,为了去寻找最好的解,被学者所提出的一种技术,但是这样的技术并不一定可以保证所得解的有效性,我们也不能肯定的说,我们用这种方法所求得的解就是最优的解。大多数情况下,我们还有可能没有办法去表达所求得解和最优解之间到底多么近似。
1.2.1国外研究现状
启发式算法出现在四十年代,它可以帮助人们去解决现实生活当中的很多组合问题。及至六到七十年代间, 随着人们对数学模型及最优解算法的重视了起来, 原先提出的启发式算法被称为“method of quick and dirty”。到了七十年代,学术理论与科学技术又得到了进一步发展,这时不考虑算法所得解与最有解的偏离程度的启发式算法再次进入到人们的视线当中。早期的启发式算法主要有一步算法[5]、2-opt算法[6]等。
八十年代初,现代智能优化算法这样的一种启发式算法开始出现并且广泛的流传。1985年,Hopfield和Tank发表了用神经网络解决TSP问题的里程碑式的论文《Neural- computation of decisions in optimization problems》,文献[7]里对Hopfield神经网主要分支:模拟退火(simulated annealing, SA)、人工神经络解决TSP问题的稳定性做了深入概述和详细研究。Sreeram[8]则采用了完全不同的切入点,从能量函数入手研究了Hopfield网络的动力学系统。提出了为什么会出现无法收敛的状况的根本原因和有关能量函数与参数的选择原则的修改意见。在此过程中,Abe[9]也对能量函数和参数的选择原则提出了自己的见解。1991年 G.C.Fox[10]首次给出了physical computation的定义和其五个网络 (artificial neural network, ANN)、确定性退火 (deterministic annealing, DA)、弹 性 网 络 (elastic network, EN)和遗传算法(genetic algorithm, GA)。虽然说一直以来NP-hard理论[11]都限制了以上这些算法只能按照启发式的思维去运行,但是随着科学家对问题不断深入地研究,无论是解的有效性还是全局最优的概率,都高于最早的启发式算法,并得到了显著的提升。正是这些进步证明对启发式算法的继续研究是值得并且有必要继续进行的。下面将从四种方法来叙述解决TSP问题的算法的发展。
模拟退火算法[12][13]是一种全局最优算法,是通过类推物理和化学的具体退火过程推理得来的,它不再局限于局部最优,而是逼近了全局最优。模拟退火算法是由退火过程和Metropolis算法[14]组成的,其中Metropolis算法是在1953年被提出的。TSP问题是模拟退火算法在状态空间离散时候的一种典型应用。
遗传算法(GA)是由Holland[15]等人在1975年提出的。GA是一种模仿了生物遗传进化的一种算法。以达尔文生物进化论为基础,后来的学者对遗传算法进行深入研究。
人工神经算法在1985年被用于解决TSP问题时取得了巨大的发展,Hopfield和Tank[7]提出的连续性Hopfield人工神经网络解决TSP问题在前人的方法上进行了改进,但是Wilson[16]等人在文献中论述证明连续性Hopfield神经网络会难以避免的陷入局部最优,而且存在着优化性能和可靠性差的问题。
蚁群算法时如今炙手可热的,继以上三种方法之后出现的一种现代启发式算法。Dorigo[17]等在二十世纪九十年代第一次提出了蚁群算法这一概念,并将这一算法用于解决TSP问题。后人又对蚁群算法不断进行完善和改进,近年来有一种比蚁群算法更加先进的被称之为自由搜索的优化算法同样的基于种群行为,其稳定性得到了很大的提高。
1.2.2国内研究现状
TSP问题不仅在外国学者之间广为流传,中国学者也对准确高效的解决TSP问题和提高算法的精准度做出了很多的贡献。1997年,郭茂祖, 洪家荣[18]在基于模拟退火算法的基础上提出了一种并行环境中解决TSP问题的方法。同年,潘立登, 黄晓峰[19]在模拟退火算法和交换算子的基础上改进了遗传算法并显著提高了算法的准确率。罗映红[20]也同样论述了用遗传算法解决TSP问题并且分析了算法的有效性。2000年,胡小兵等[21]提出了用遗传算法解决TSP问题的一种改进的算法,即和传统的遗传算法相比,他们在研究的时候加入了“幼代”这样一个概念,然后还对生长过程进行模拟研究,借此来提高求解的有效性。神经网络方面,周江鸣[22]在其文章中用玻尔兹曼神经网络解决了旅行商问题。党建武, 靳蕃[23]分析了有关多路径旅行商的问题,根据不同情况对问题进行了分类并且提出了智能化的高效解决办法。姜国均[24]则提出了一种用Hopfield神经网络解决旅行商问题的一种改进的算法。蚁群算法作为一种新兴的热门算法,中国学者董梅, 谢楠琳[25]对蚁群算法提出改进意见并用改进后方法去解决景点群的最优路径选择问题。曹浪财等[26]则创新的论述改进传统蚁群算法提出智能蚁群算法,大大减少了求解的计算量。
1.3论文研究内容及技术路线
1.3.1研究内容
1.界定TSP问题,阐述TSP问题研究现状
2.人工神经网络及Hopfield神经网络简介
3.采用Hopfield实现TSP问题的同时利用LINGO解决TSP问题,对两种方法进行分析比对
1.3.2研究目标
本论文旨在分析Hopfield神经网络算法解决TSP问题的理论过程,并用MATLAB和LINGO两种软件求解结果进行分析比较。
1.3.3技术路线
1.给出TSP问题的具体描述及数学模型。
2.介绍神经网络应用于TSP问题的相关理论知识及Hopfield算法在求解TSP问题中的应用分析。
3.通过MATLAB与LINGO两种软件进行求解,结合实际给出Hopfield算法解决TSP问题的分析。
1.4本章小结
本章论述了TSP问题自提出到被解决的发展历程,提及到了发展至今,能解决TSP问题的各种方法和这些方法的基本概况,最后强调了Hopfield神经网络对于TSP问题解决的重要意义。
第2章TSP问题
2.1 TSP问题简述
组合最优化问题[5](全称Combinatorial Optimization Problem)通常被人们简称为COP。COP指的是在给定了约束条件的情况之下,求使给定目标函数得到最大值或者是最小值的解答。组合最优化问题是运筹学中不可忽视的一个经典问题,因为它通过对数学方法的探寻去确定所求问题的顺序、排列、筛选或分组。这样的特性也使得组合最优化问题被广泛应用于生活中的各个领域比如说通信网络、信息科学和工程管理等。总的来说,对组合最优化问题的探寻以及对组合最优化问题数学解决方法的改进都有着极其重要的意义。
TSP问题是熟知的计算路径更优的问题,即旅行商问题(全称Traveling Salesman Problem)。TSP问题可以被简单的描述为一个旅行商欲遍历n个城市并且每个城市只可以经过一次,最后回到出发城市,求怎样规划路径可以使总路径最短。旅行商问题是组合最优化问题的代表性难题,虽然我们可以引用上述的简要语言去概括TSP问题,但其实,TSP是很多其他问题的缩影,比如说当电焊工焊一块铁板时,他选择焊点的顺序不同,路径长度也会有所不同。
TSP被认为是一个np问题,即当旅行商需要去到n个城市时,我们可以把他对线路的选择看作是对n个城市的一种排列组合,那么此时线路存在的数量是n!条。随着城市数量的增长,线路数会呈指数式爆炸增长,但是需要注意的是,同样的两个城市,不同的顺序是完全一样的,所以实际上线路的条数是Rn=n!/2n。当n=5时,R5=12,当n=6时,R6=120,而当n=100时,R100=4.67×10155,从急剧变大的数据可以看出,当n较小时还可以用简单的穷举解决的问题,遇到n较大的情况则已经无法适用。
2.2 TSP问题的数学模型
因为TSP问题所求的核心问题是推销员所经历的行程最短,故需要使下面式(2.1)中的目标函数最小。其中,城市号被用 来表示,取值来自
来表示,取值来自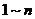 之间的自然数。两个城市
之间的自然数。两个城市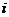 和
和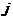 之间的距离可以用来表示,且本论文主要研究对象为对称式的TSP问题,所以有。
之间的距离可以用来表示,且本论文主要研究对象为对称式的TSP问题,所以有。
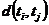
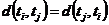
(2.1)

上述语言还可以被描述为,从赋权完全的图中找到一个拥有最小权值的哈密顿图。令顶点集为,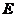 是其边集,为赋权完全图,且已知各个顶点之间的距离,设:
是其边集,为赋权完全图,且已知各个顶点之间的距离,设:
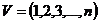
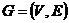
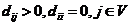
(2.2)
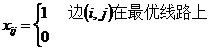
TSP问题的数学模型为:
(2.3)
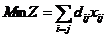
(2.4)
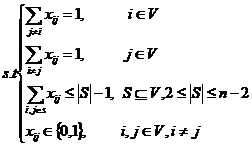
式(2.4)中的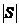 指的是集合
指的是集合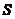 里面包含图
里面包含图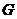 顶点的个数。上式中有四个式子,第一个约束表示:对于每个顶点,只允许有一条边进,同样的,也只能允许有一条边出。第二个约束表示:不会存在任何子回路解。总而言之,当上面的所有的约束条件被满足了之后,我们所得到的解,一条完整的穿过全部顶点的哈密顿回路就被构成。
顶点的个数。上式中有四个式子,第一个约束表示:对于每个顶点,只允许有一条边进,同样的,也只能允许有一条边出。第二个约束表示:不会存在任何子回路解。总而言之,当上面的所有的约束条件被满足了之后,我们所得到的解,一条完整的穿过全部顶点的哈密顿回路就被构成。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: